4 Conditional Logic
Updated for S2026? No.
The first big addition to “basic” R that we are going to make is the ability to make conditional statements. This is going to allow us, for example, to look at or alter certain parts of a dataset based on a particular condition. If we had a dataset of all counties in the United States, we might be interested in a question like: What is the average median income of counties in the South? These conditional logic statements will let us answer those questions. (And do a whole lot more!)
4.1 Boolean Variables
As a bridge to get to conditional logic statements we first have to learn about a new variable type: “Boolean” variables. This is just a fancy way that R refers to variables that take on the values of TRUE and FALSE.
If we give R a statement that can be either true or false, it will return the right value:
2 == 1+1
#> [1] TRUE
2 == 2+2
#> [1] FALSEA couple of things to note here. First, we use a double equals sign for conditional logic statements. A single equals sign is used for assignment (we have used <- as out assignment operator, but you can also use =. I like using the arrow so I don’t get confused about what i’m doing). Second, while TRUE and FALSE are words, they are not in quotation marks. This is not the words “True” and “False”, R is treating these as special values, not just characters.
The statements we have to give R have to be exactly true. So for example:
2/3== .666
#> [1] FALSEIs false, because the right hand side is a rounded approximation of the left hand side.
We can see if things are strictly equal, but can also see if something is greater or less than a particular value:
2>3
#> [1] FALSE
2<3
#> [1] TRUEOr if something is less/greater than or equal to another thing:
2<=2
#> [1] TRUE
2>=3
#> [1] FALSEQuite helpfully, R will also perform the test on all entries in a particular vector. So if we have a vector and want to determine which entries are equal to 3:
vec <- c(1,2,3,4,5)
vec == 3
#> [1] FALSE FALSE TRUE FALSE FALSEOr which vectors are greater than or equal to 3:
vec >= 3
#> [1] FALSE FALSE TRUE TRUE TRUER returns TRUE for all entries that are true, and FALSE for all entries that are false.
If this seems a bit silly now, remember that we are rapidly moving to a world where we are going to have datasets with thousands or tens of thousands of rows. Here I can eyeball which entries of vec are true or false, but in big datsets I won’t be able to, for example, eyeball which counties are in the south.
One of the cool things about boolean variables is that R mathematically treats TRUE as 1 and FALSE as 0.
This is cool because we can quickly determine the number of true entries using sum()
vec >= 3
#> [1] FALSE FALSE TRUE TRUE TRUE
sum(vec >= 3)
#> [1] 3That means we can also figure out the proportion of true entries by taking the mean of a boolean variable:
mean(vec >= 3)
#> [1] 0.6This is going to keep coming up so let’s take a second to prove to ourselves that taking the mean of a variable that is 0 or 1 returns the proportion of 1s.
consider this vector:
\[ v = \lbrace 0,1,1\rbrace \]
We want to take the mean of this vector. The formula for the mean is:
\[ \bar{v} = \frac{\sum v_i}{n} \]
Which just means: add up all of the value of the vector and divide by the number of values. So for this variable:
\[ \bar{v} = \frac{0 + 1+ 1}{3}\\ \bar{v} = \frac{2}{3}\\ \]
We can see really clearly that what is going to happen here is that the numerator will equal the number of 1 and the denominator witll be the total length of the vector. So the mean will return the proportion of entries that equal 1. Or, if we have a boolean variable (which treats T=1 and F=0) the proportion of the entries that are true. We are going to make use of this fact a lot!
Another key boolean operator is the exclamation point, which we use in two distinct ways. First, we use it simply to say “not equal”:
2!=3
#> [1] TRUEWe can also use it in front of any logical statement to negate the whole thing, turning all TRUE to FALSE and vice versa:
vec==3
#> [1] FALSE FALSE TRUE FALSE FALSE
!(vec==3)
#> [1] TRUE TRUE FALSE TRUE TRUEWhy is this helpful? Imagine a situation where you have data on all counties in the US and you want to look at all the values except those in Alaska. It is way easier to say “not Alaska” than it is to say “Arizona, Alabama, Arkansas, Connecticut….”.
The final boolean operator we will make use of is %in%, which is maybe the most helpful one. This will test whether things on the left hand side are present in the right hand side. The logical test is being performed on the things in the left hand side.
So if we have the following vecotr and want to see if 3 is in that vector we can do:
vec <- 1:10
3 %in% vec
#> [1] TRUEThis is different from:
3==vec
#> [1] FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE FALSE
#> [10] FALSEWhich will tell us when vec is equal to 3. The %in% command just tells us if 3 is in the vector.
This is particularly helpful when we have two vectors and want to see what elements of one vector are in the other:
vec1 <- 1:30
vec2 <- 25:50
vec1 %in% vec2
#> [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
#> [10] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
#> [19] FALSE FALSE FALSE FALSE FALSE FALSE TRUE TRUE TRUE
#> [28] TRUE TRUE TRUEThe last 5 entries to vec, 25,26,27,28,29,30 are in vec2.
Note that this is not a symmetrical command, such that this gives us a different result:
vec2 %in% vec1
#> [1] TRUE TRUE TRUE TRUE TRUE TRUE FALSE FALSE FALSE
#> [10] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
#> [19] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE4.2 Using Boolean Variables to Subset
How do we use these boolean variables to subset? Let’s load in the small table of population figures from last week:
library(rio)
population.table <- import("https://github.com/marctrussler/IDS-Data/raw/main/populationtable.Rds")
#> Warning: Missing `trust` will be set to FALSE by default
#> for RDS in 2.0.0.I’m going to pull out just the emissions information, which is the 4th column:
emissions <- population.table[,4]
emissions
#> [1] 6.00 9.33 14.83 19.37 22.70 25.12 33.13We have learned that we can extract a range of values using their index position:
emissions[4:7]
#> [1] 19.37 22.70 25.12 33.13The other way we can extract information from a vector is to put in the square brackets a vector of TRUE and FALSE. R will return the index positions of the TRUE values and not return the index positions of the FALSE values. Note that we can also shorthand TRUE to T and FALSE to F.
emissions[c(F,F,F,T,T,T,T)]
#> [1] 19.37 22.70 25.12 33.13This returned the 4th, 5th, 6th, and 7th index positions, which correspond to the fact that the vector we entered had T for those same positions.
You should see where this is going: if we can enter a vector of trues and falses in the square brackets to only return certain values, than we can use a boolean variable there to do that job.
So how might I return the values of emissions that are less than 20?
First let’s identify which entries those are:
emissions<20
#> [1] TRUE TRUE TRUE TRUE FALSE FALSE FALSEThe 1st through 4th entries are evaluated as true using that logic statement. But this expression generates a vector that is the same length of emissions that gives us the info of which index position satisfies our criteria. As such, we can do:
emissions[emissions<20]
#> [1] 6.00 9.33 14.83 19.37I would read that expression as: give me the values of emissions where emissions are less than 20.
What if I want to return the values of world pop that are greater than 4000?
world.pop <- population.table[,2]
world.pop[world.pop>4000]
#> [1] 4449 5320 6127 6916That’s very helpful!
We saw last week that we can use the square brackets to return certain rows or certain columns, and we can similarly use conditional logic to return rows that meet a certain condition.
If I want to return the rows where emissions are less than 20:
population.table[emissions<20,]
#> year world.pop pop.rate emissions
#> [1,] 1950 2525 1.000000 6.00
#> [2,] 1960 3026 1.198416 9.33
#> [3,] 1970 3691 1.461782 14.83
#> [4,] 1980 4449 1.761980 19.37Remember the use of the comma here! What we are subsetting is a matrix with 2 dimensions, so we have to give information on which columns we want to return. By putting a comma and leaving the second part blank, we are saying “give me all the columns”.
Let’s do the same for world pop greater than 4000, but instead of using the world.pop variable I generated, I will simply make use of the fact that the 2nd column is world population:
population.table[population.table[,2]>4000,]Why might that be a preferable thing to do? Let’s look what happens when we put a boolean variable in the square brackets that is too long:
#Uncomment and try to run:
#population.table[c(T,T,F,F,F,F,F,T,T,F,F),]If we do a logical statement that is too short it will repeat it to make it the right length
population.table[c(T,F,F),]
#> year world.pop pop.rate emissions
#> [1,] 1950 2525 1.00000 6.00
#> [2,] 1980 4449 1.76198 19.37
#> [3,] 2010 6916 2.73901 33.13So while that produces output it does so in a convuluted and slightly unpredictable way. (Unpredictable because I truly didn’t know what R was going to do before I wrote these previous lines. I figured it out, but only because this is a short dataset).
So best practice is definitely to have a boolean string that is exactly the same length as the number of rows of our matrix (or the number columns, if that’s what we are sub-setting to). If we write our logical statement based off of one of the columns, we are guaranteed to have the right number of rows!
We don’t have to make use of hard-coded conditions. We may want, for example, to return the population table when emissions is greater than its median value:
population.table[population.table[,4]> median(population.table[,4]),]
#> year world.pop pop.rate emissions
#> [1,] 1990 5320 2.106931 22.70
#> [2,] 2000 6127 2.426535 25.12
#> [3,] 2010 6916 2.739010 33.13With the same logic we can make use of the %in operator. As long as we are producing a vector of trues and falses the same length as the thing we are subsetting R will return the right thing.
For example, I may be interested in considering the overlapping group memberships of Buffalo Springfield; Crosby, Stills, and Nash; and Crosby, Stills, Nash, and Young. Look I know these aren’t the most relevant bands to you, but if you’re so cool why aren’t you writing this textbook?
buffalo.springfield <- c("stills", "martin","palmer","furay","young")
csn <- c("crosby","stills","nash")
csny <- c("crosby","stills","nash","young")We can create boolean variables to tell us which members of Buffalo Springfield are in CSN, and which are in CSNY:
buffalo.springfield %in% csn
#> [1] TRUE FALSE FALSE FALSE FALSE
buffalo.springfield %in% csny
#> [1] TRUE FALSE FALSE FALSE TRUEAnd simply putting those Boolean variables into square brackets will return the members of Buffalo Springfield that are in each band.
buffalo.springfield[buffalo.springfield %in% csny]
#> [1] "stills" "young"
buffalo.springfield[!(buffalo.springfield %in% csny)]
#> [1] "martin" "palmer" "furay"Does this give the same result? Does this make sense?
buffalo.springfield[csny %in% buffalo.springfield]
#> [1] "martin" "furay"Now all of these examples have been super obvious. Things we can eyeball. I did this on purpose so you can go slowly and see exactly what each command is doing. But again, try to think about how helpful these tools are going to be when we have thousands of observations.
4.3 And/Or
There are times where we may be interested in multiple conditions at once. To do that we can string together booleans with & (and) as well as | (or).
These two operators are super helpful, but can sometimes be a bit hard to keep seperate and to determine when you have to use each.
Let’s look at what happens when we string together boolean statements with an &:
#Both statements are T
(2 == 2) & (3 == 3)
#> [1] TRUE
#One of the statements is T, the other F
(2 == 2) & (3 == 2)
#> [1] FALSE
#Both statements are F
(2 == 4) & (3 == 2)
#> [1] FALSEThe & operator gives us only one T or F back. It returns a T if ALL the pieces of the statement are true, and a F if ANY of the statemens are false. This remains the same if we add more pieces:
#All are T
(2 == 2) & (3 == 3) & (2>1) & ("yes" %in% c("yes","no"))
#> [1] TRUE
#Two are false
(2 == 2) & (3 == 3) & (2<1) & ("maybe" %in% c("yes","no"))
#> [1] FALSENow let’s look at the | operator:
#Both statements are T
(2 == 2) | (3 == 3)
#> [1] TRUE
#One of the statements is T, the other F
(2 == 2) | (3 == 2)
#> [1] TRUE
#Both statements are F
(2 == 4) | (3 == 2)
#> [1] FALSEThe or operator returns T if ANY of the pieces are true. To return a false ALL of the pieces have to be false.
This is – helpfully and somewhat obviously – also just how our language works.
These and/or statements will be particularly helpful in subsetting to particular cases we may want to examine or do further math on.
Return the rows of the population table where world pop is greater than 4000 and emissions are greater than 20:
population.table[population.table[,2] > 4000 & population.table[,4] >20,]
#> year world.pop pop.rate emissions
#> [1,] 1990 5320 2.106931 22.70
#> [2,] 2000 6127 2.426535 25.12
#> [3,] 2010 6916 2.739010 33.13What does this return:
population.table[population.table[,2] > 4000 | population.table[,4] >20,]
#> year world.pop pop.rate emissions
#> [1,] 1980 4449 1.761980 19.37
#> [2,] 1990 5320 2.106931 22.70
#> [3,] 2000 6127 2.426535 25.12
#> [4,] 2010 6916 2.739010 33.13Because this is an OR statement we will get any row where either of these statements are true, as opposed to rows where both of them have to be true.
4.4 A problem is encountered
These statements also work well when we have a “categorical” variable: a variable that splits cases into different bins. (As opposed to the continuous variables we have now).
Let’s say I add a variable which is my subjective rating of the music quality of each of these decades, for which I am using the complex rating scale of good bad meh.
music <- c("meh","good","meh","bad","good","bad","good")#Let’s try to add this to our little dataset
population.table.new <- cbind(population.table, music)What did we get?
population.table.new
#> year world.pop pop.rate emissions music
#> [1,] "1950" "2525" "1" "6" "meh"
#> [2,] "1960" "3026" "1.19841584158416" "9.33" "good"
#> [3,] "1970" "3691" "1.46178217821782" "14.83" "meh"
#> [4,] "1980" "4449" "1.7619801980198" "19.37" "bad"
#> [5,] "1990" "5320" "2.10693069306931" "22.7" "good"
#> [6,] "2000" "6127" "2.42653465346535" "25.12" "bad"
#> [7,] "2010" "6916" "2.7390099009901" "33.13" "good"At first glance this looks ok, but notice that everything is in quotation marks! Here we are bumping against the limitations of the simple matricies we have been building the the cbind command. When we use these simple matricies all of the data can only be of one class (numeric, or character, or boolean etc.). When we attempted to add a character vector R was forced to treat the whole table as character information.
So if we tried to do
mean(population.table.new[,2])
#> Warning in mean.default(population.table.new[, 2]):
#> argument is not numeric or logical: returning NA
#> [1] NANothing!
The fix to this is very easy, and has us look ahead to our content for next week. Instead of a simple matrix we will instead create a data frame which is a special sort of matrix that allows us to be much more flexible with the types of data we can combine. This will be the primary way in which we store and view data in this class.
If we want to cbind our data together in a way that will preserve the different classes of the data, we just need to tell R we want a data frame with:
population.table <- cbind.data.frame(population.table,music)
population.table
#> year world.pop pop.rate emissions music
#> 1 1950 2525 1.000000 6.00 meh
#> 2 1960 3026 1.198416 9.33 good
#> 3 1970 3691 1.461782 14.83 meh
#> 4 1980 4449 1.761980 19.37 bad
#> 5 1990 5320 2.106931 22.70 good
#> 6 2000 6127 2.426535 25.12 bad
#> 7 2010 6916 2.739010 33.13 goodWhy do we even have simple matrices if data frames are better? The short answer for now is that there is a lot of extra information contained in a data frame which means extra storage. When we get very large datasets extra informaiton may slow things down. It’s nice to have an option that is inherantly lower memory.
So now, can we determine the rows in which music was good or meh?
population.table[population.table[,5]=="good" | population.table[,5]=="meh",]
#> year world.pop pop.rate emissions music
#> 1 1950 2525 1.000000 6.00 meh
#> 2 1960 3026 1.198416 9.33 good
#> 3 1970 3691 1.461782 14.83 meh
#> 5 1990 5320 2.106931 22.70 good
#> 7 2010 6916 2.739010 33.13 goodAlternatively, we could do:
population.table[population.table[,5] %in% c("good","meh"),]
#> year world.pop pop.rate emissions music
#> 1 1950 2525 1.000000 6.00 meh
#> 2 1960 3026 1.198416 9.33 good
#> 3 1970 3691 1.461782 14.83 meh
#> 5 1990 5320 2.106931 22.70 good
#> 7 2010 6916 2.739010 33.13 goodWhat if we wanted all the years that were bad?
For demonstration, note that we can do this:
population.table[!(population.table[,5]=="good" | population.table[,5]=="meh"),]
#> year world.pop pop.rate emissions music
#> 4 1980 4449 1.761980 19.37 bad
#> 6 2000 6127 2.426535 25.12 badBut really we would do:
population.table[population.table[,5]=="bad",]
#> year world.pop pop.rate emissions music
#> 4 1980 4449 1.761980 19.37 bad
#> 6 2000 6127 2.426535 25.12 badWhat would happen if we did the original command with & instead of | ?
population.table[population.table[,5]=="good" & population.table[,5]=="meh",]
#> [1] year world.pop pop.rate emissions music
#> <0 rows> (or 0-length row.names)Nothing! And thinking through that command logically it doesn’t make much sense. Which rows satisfy both of those conditions? None of them.
Let’s try to answer some more complicated logical statements
What are the cases where world.pop is above is over 3000 and the decade’s music was wither meh or good?
population.table[population.table[,2]>3000
& population.table[,5]=="meh"
| population.table[,5]=="good",]
#> year world.pop pop.rate emissions music
#> 2 1960 3026 1.198416 9.33 good
#> 3 1970 3691 1.461782 14.83 meh
#> 5 1990 5320 2.106931 22.70 good
#> 7 2010 6916 2.739010 33.13 goodThis worked, but I start to get worried about order of operations when I have long strings of logical statements going at once. Is R thinking about this in the same way as I am?
For example what If I re-arrange the above statements?
population.table[ population.table[,5]=="meh"
| population.table[,5]=="good"
& population.table[,2]>3000,]
#> year world.pop pop.rate emissions music
#> 1 1950 2525 1.000000 6.00 meh
#> 2 1960 3026 1.198416 9.33 good
#> 3 1970 3691 1.461782 14.83 meh
#> 5 1990 5320 2.106931 22.70 good
#> 7 2010 6916 2.739010 33.13 goodThis, indeed, gave us a different answer then what we got above. Where before we are saying give me cases where pop is greater than 3000 AND (music is either meh or good), Now we have music is meh OR (music is good and pop is over 3000).
The best way to be be careful about this is to use parenthesese, asyou would in math, to keep statements together.
So for example deploying some parentheses:
population.table[(population.table[,5]=="meh"
| population.table[,5]=="good")
& population.table[,2]>3000,]
#> year world.pop pop.rate emissions music
#> 2 1960 3026 1.198416 9.33 good
#> 3 1970 3691 1.461782 14.83 meh
#> 5 1990 5320 2.106931 22.70 good
#> 7 2010 6916 2.739010 33.13 goodGives us the right answer.
And if I was doing the first one I would still use them just to be careful:
population.table[population.table[,2]>3000
& (population.table[,5]=="meh"
| population.table[,5]=="good"),]
#> year world.pop pop.rate emissions music
#> 2 1960 3026 1.198416 9.33 good
#> 3 1970 3691 1.461782 14.83 meh
#> 5 1990 5320 2.106931 22.70 good
#> 7 2010 6916 2.739010 33.13 goodNote that you could alternatively use the %in% operator for this:
population.table[population.table[,2]>3000
& (population.table[,5] %in% c("meh","good")),]
#> year world.pop pop.rate emissions music
#> 2 1960 3026 1.198416 9.33 good
#> 3 1970 3691 1.461782 14.83 meh
#> 5 1990 5320 2.106931 22.70 good
#> 7 2010 6916 2.739010 33.13 goodOne more complex one: What are cases where emissions are less than the median, music is either bad or meh, and population rate is less than 2?
population.table[population.table[,4] < median(population.table[,4])
&(population.table[,5]=="bad" | population.table[,5]=="meh")
& population.table[,3] <2,]
#> year world.pop pop.rate emissions music
#> 1 1950 2525 1.000000 6.00 meh
#> 3 1970 3691 1.461782 14.83 meh4.5 Plotting with Conditional Logic
To look at some more complicated/interesting plots, we are going to load in some data on all of the counties in Pennsylvania.
#Note that we've already loaded the rio package in the code above. We shouldn't have to load it again.
pa.counties <- import("https://github.com/marctrussler/IDS-Data/raw/main/PACounties.Rds")
#> Warning: Missing `trust` will be set to FALSE by default
#> for RDS in 2.0.0.
head(pa.counties)
#> population population.density median.income
#> [1,] 61304 53.42781 51457
#> [2,] 626370 1036.30200 86055
#> [3,] 123842 235.53000 47969
#> [4,] 41806 42.69485 46953
#> [5,] 112630 167.45910 48768
#> [6,] 46362 112.79050 47526
#> percent.college percent.transit.commute
#> [1,] 17.84021 0.2475153
#> [2,] 40.46496 3.4039931
#> [3,] 20.80933 1.1913318
#> [4,] 18.14864 0.9152430
#> [5,] 22.55270 0.4175279
#> [6,] 12.47843 0.3038048For each of the 67 counties we have data on population, population density, median income, percent of residents with a college degree, and the percent of people who commute by transit.
Let’s generate a scatterplot which looks at the relationship between the percent of residents with a college degree and the median income of the county:
plot(pa.counties[,4], pa.counties[,3],
xlab="Percent with College Degree",
ylab="Median Income",
main="College Degree Attainment vs. Household Income in PA",
pch=16)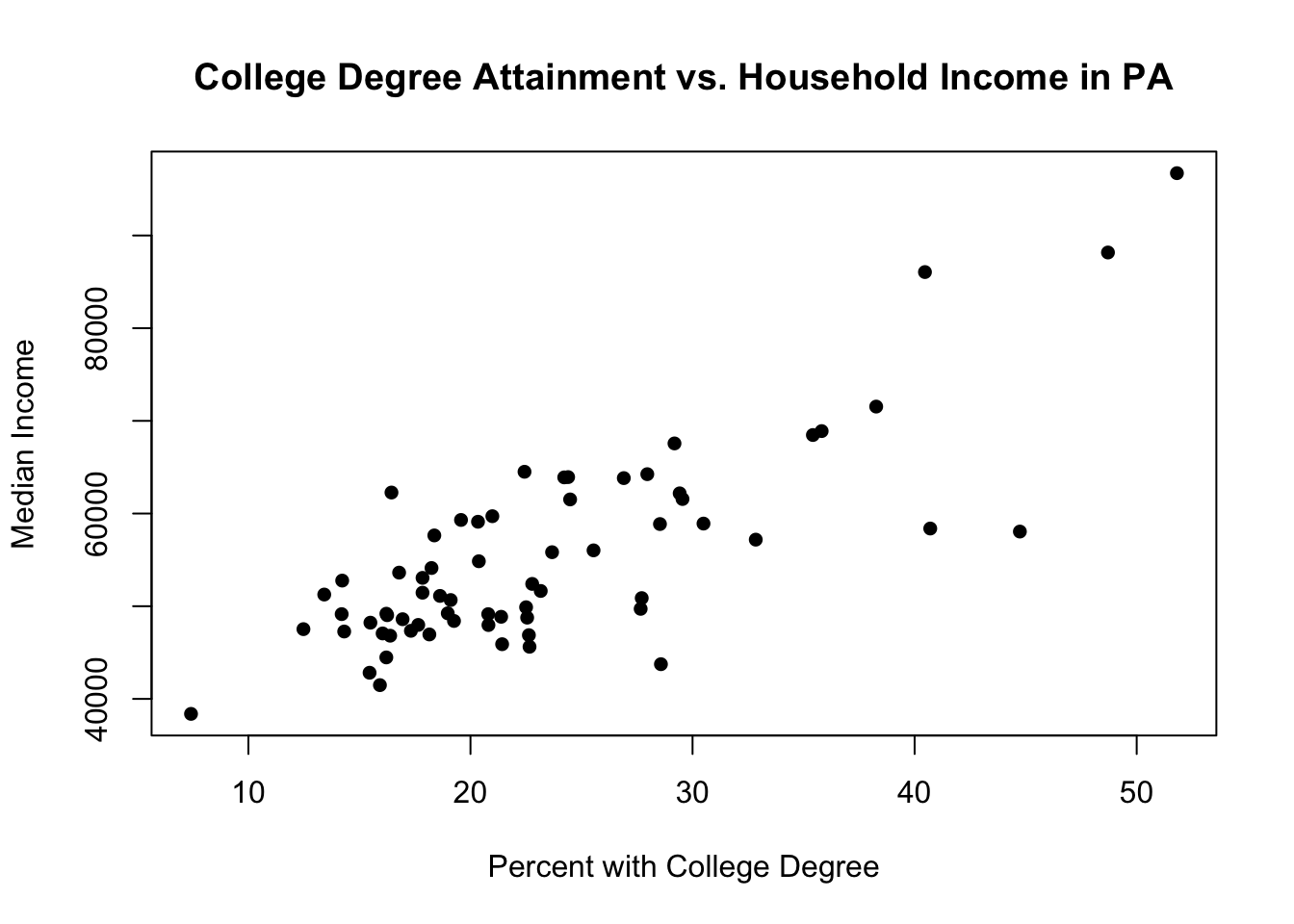
How would you describe what you are seeing here?
Maybe I think that this relationship is different in rural and non-rural places. It’s possible that the impact of having a college degree is greater in urban areas than in rural areas, the latter having many well-paying hands-on professions that don’t require a college degree.
First let’s identify the cases that are rural, which I will define as having a population density under 100 people per square mile:
#Rural
pa.counties[pa.counties[,2]<100,]
#> population population.density median.income
#> [1,] 61304 53.42781 51457
#> [2,] 41806 42.69485 46953
#> [3,] 4686 11.82644 41485
#> [4,] 38827 64.62159 45625
#> [5,] 80216 70.07706 47270
#> [6,] 39074 44.00304 49234
#> [7,] 86164 85.11690 49144
#> [8,] 30608 36.99472 51112
#> [9,] 7351 17.20458 38383
#> [10,] 14506 33.15268 51259
#> [11,] 37144 64.49182 54121
#> [12,] 45421 51.93039 48597
#> [13,] 44084 67.56878 46818
#> [14,] 24562 62.76217 52765
#> [15,] 114859 93.47616 52407
#> [16,] 48611 48.02024 49146
#> [17,] 52376 77.67646 47982
#> [18,] 40035 45.28136 48409
#> [19,] 45924 83.27888 62266
#> [20,] 16937 15.66323 42821
#> [21,] 74949 69.76122 48224
#> [22,] 6177 13.72851 47346
#> [23,] 41340 50.20061 53059
#> [24,] 41226 36.36177 50667
#> [25,] 51536 71.02713 54851
#> [26,] 27588 69.43777 59308
#> percent.college percent.transit.commute
#> [1,] 17.840213 0.24751533
#> [2,] 18.148636 0.91524296
#> [3,] 15.922330 0.19175455
#> [4,] 22.659126 0.07535358
#> [5,] 14.313682 0.25832032
#> [6,] 18.976917 0.10842273
#> [7,] 20.798972 0.56715785
#> [8,] 18.627626 0.64111126
#> [9,] 7.415991 0.11876485
#> [10,] 13.414867 0.12279355
#> [11,] 18.245268 0.13294151
#> [12,] 16.943197 0.19342360
#> [13,] 16.384343 0.55206257
#> [14,] 14.223411 0.36993594
#> [15,] 22.779329 1.21918897
#> [16,] 14.199644 0.52631579
#> [17,] 17.648291 0.45625335
#> [18,] 19.257541 0.25280899
#> [19,] 16.442314 0.38271550
#> [20,] 15.456636 0.01525553
#> [21,] 15.494020 0.10321209
#> [22,] 17.317867 0.03800836
#> [23,] 17.841467 0.12268570
#> [24,] 19.109176 0.74451411
#> [25,] 20.376288 1.00570544
#> [26,] 19.573969 0.53312426
#Suburban-Urban
pa.counties[pa.counties[,2]>=100,]
#> population population.density median.income
#> [1,] 626370 1036.3020 86055
#> [2,] 123842 235.5300 47969
#> [3,] 112630 167.4591 48768
#> [4,] 46362 112.7905 47526
#> [5,] 167586 275.5184 63931
#> [6,] 821301 1700.5640 88166
#> [7,] 18294 140.4612 57183
#> [8,] 301778 816.3982 67565
#> [9,] 92325 201.5822 47063
#> [10,] 186566 236.5803 68472
#> [11,] 134550 195.4642 45901
#> [12,] 63931 167.5954 53624
#> [13,] 161443 145.4622 58055
#> [14,] 517156 689.0596 96726
#> [15,] 66220 137.0712 49889
#> [16,] 247433 453.5899 68895
#> [17,] 274515 522.9787 58916
#> [18,] 563527 3065.6680 71539
#> [19,] 275972 345.3604 49716
#> [20,] 132289 167.3827 44476
#> [21,] 153751 199.1018 59713
#> [22,] 85755 103.6350 46877
#> [23,] 211454 460.9121 50875
#> [24,] 538347 570.3637 63823
#> [25,] 87382 243.9609 48860
#> [26,] 138674 383.2833 59114
#> [27,] 362613 1050.4340 62178
#> [28,] 317884 357.0345 51646
#> [29,] 102023 196.6667 64507
#> [30,] 1225561 1678.5810 58383
#> [31,] 66331 101.5511 49032
#> [32,] 166896 383.9213 55828
#> [33,] 416642 486.5211 61522
#> [34,] 45114 142.7855 56026
#> [35,] 1575522 11737.2300 43744
#> [36,] 55498 101.8386 64247
#> [37,] 143555 184.3684 49190
#> [38,] 40466 123.0781 57638
#> [39,] 354751 345.0750 58866
#> [40,] 207547 242.1817 61567
#> [41,] 444014 491.0540 63902
#> percent.college percent.transit.commute
#> [1,] 40.46496 3.4039931
#> [2,] 20.80933 1.1913318
#> [3,] 22.55270 0.4175279
#> [4,] 12.47843 0.3038048
#> [5,] 24.39716 4.6309469
#> [6,] 48.70617 5.4573510
#> [7,] 32.84628 0.5448644
#> [8,] 29.18657 1.8935534
#> [9,] 16.04418 0.3488656
#> [10,] 35.41892 0.6410256
#> [11,] 21.42523 1.1256801
#> [12,] 16.78638 1.0114351
#> [13,] 44.73959 5.4720745
#> [14,] 51.81124 2.7324237
#> [15,] 22.50467 0.1946243
#> [16,] 35.81391 0.8001549
#> [17,] 30.49271 2.5856530
#> [18,] 38.26926 10.6107110
#> [19,] 27.66328 2.0223694
#> [20,] 16.21057 0.3391212
#> [21,] 20.98520 0.1572809
#> [22,] 22.63036 0.9008264
#> [23,] 27.71136 1.0287237
#> [24,] 26.90383 1.2779637
#> [25,] 21.38177 0.9397328
#> [26,] 20.33872 0.9104957
#> [27,] 29.41977 2.0980148
#> [28,] 23.16397 1.1524775
#> [29,] 22.43348 0.3312671
#> [30,] 40.70367 9.5237552
#> [31,] 16.24861 0.6939673
#> [32,] 23.67465 1.9794151
#> [33,] 24.48689 1.7497149
#> [34,] 25.54195 0.1885119
#> [35,] 28.57581 25.3335280
#> [36,] 27.96192 2.6365581
#> [37,] 16.21310 0.6844193
#> [38,] 18.37173 0.1265823
#> [39,] 28.53210 1.1383971
#> [40,] 29.54739 1.5549823
#> [41,] 24.22166 0.8166524Now I want two sets of dots, one for rural and one for non-rural. We can easily do this in steps, plotting first the rural counties and then on-top of that the non rural counties:
How to can we modity the original code to only include rural?
Does this work? Why not?
#Uncomment and run:
#plot(pa.counties[pa.counties[,2]<100,4], pa.counties[,3],
# xlab="Percent with College Degree",
# ylab="Median Income",
# main="College Degree Attainment vs. Household Income in PA",
# pch=16)No! That won’t work because we only subset the x values. For a scatterplot we need x and y coordinates for each point, so the two vectors have to be the same length.
So subsetting both vectors:
plot(pa.counties[pa.counties[,2]<100,4], pa.counties[pa.counties[,2]<100,3],
xlab="Percent with College Degree",
ylab="Median Income",
main="College Degree Attainment vs. Household Income in PA",
pch=16)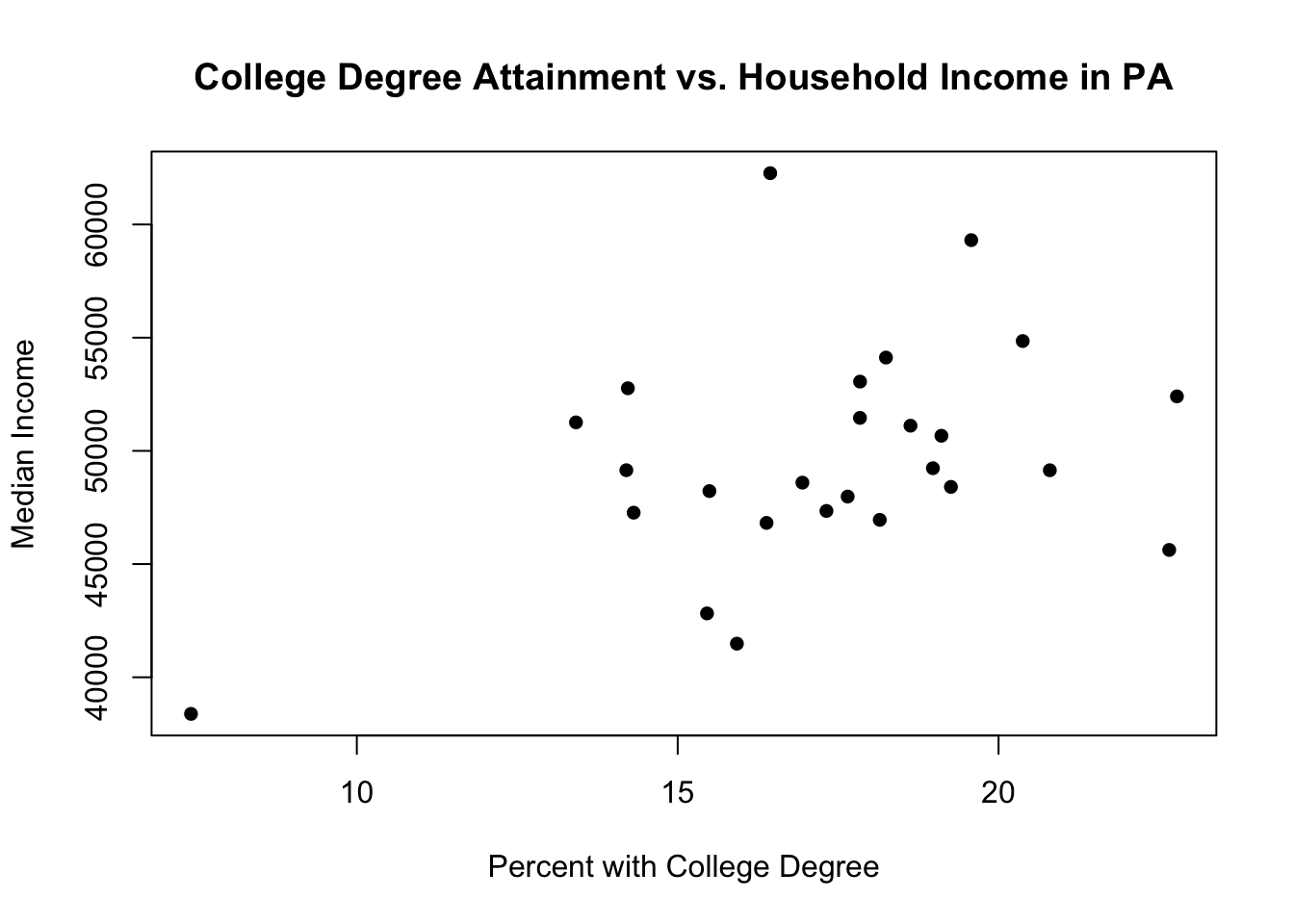
Those are the rural counties. To put the urban counties in we can use the points command, which allows us to add additional points to an already existing scatterplot created with plot
plot(pa.counties[pa.counties[,2]<100,4], pa.counties[pa.counties[,2]<100,3],
xlab="Percent with College Degree",
ylab="Median Income",
main="College Degree Attainment vs. Household Income in PA",
pch=16)
points(pa.counties[pa.counties[,2]>=100,4], pa.counties[pa.counties[,2]>=100,3],
pch=16)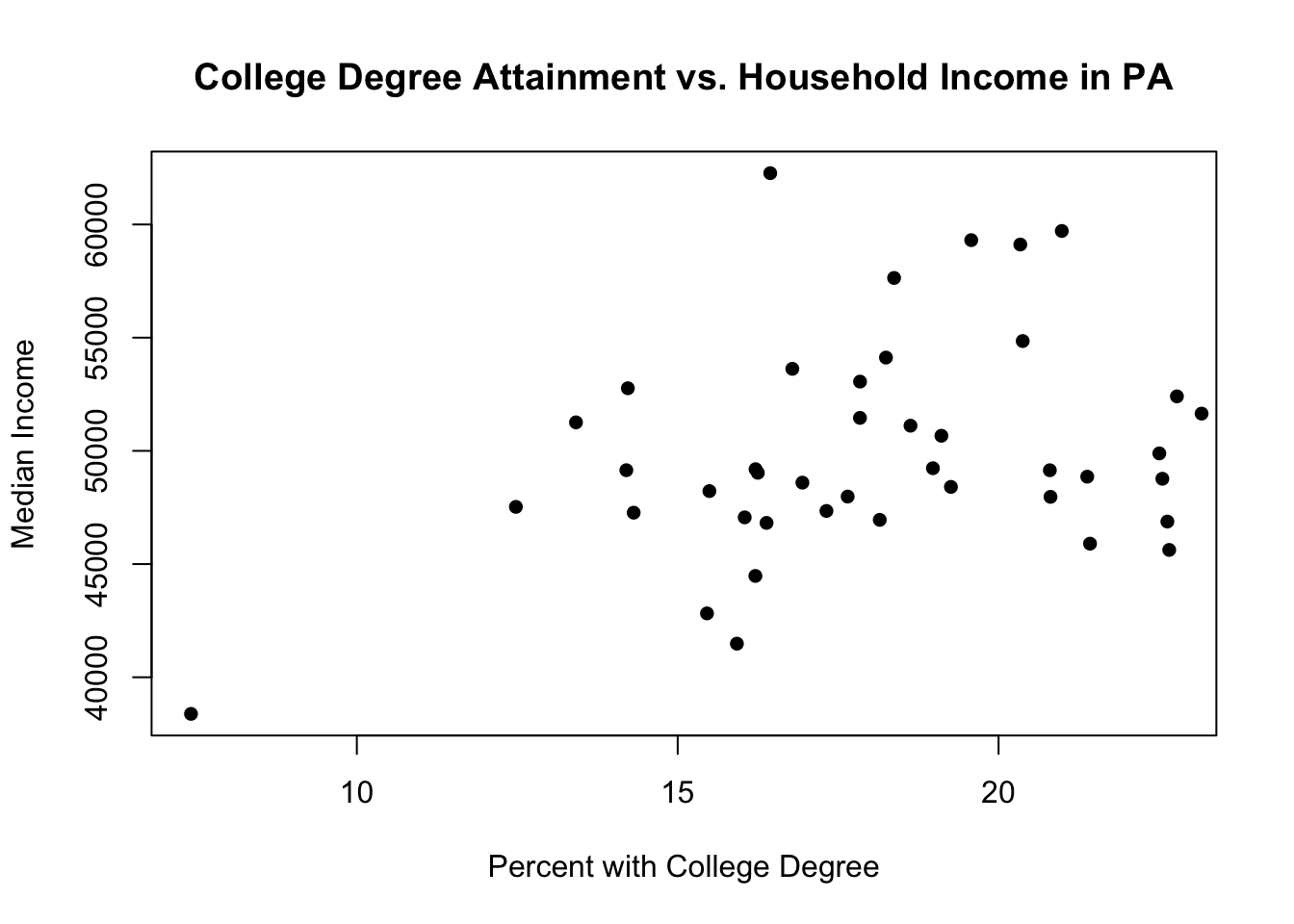
Well that just looks like our original plot! The points for rural and non-rural are the same color and type, so we can’t differentiate them.
So we can change the type of the second set of points:
plot(pa.counties[pa.counties[,2]<100,4], pa.counties[pa.counties[,2]<100,3],
xlab="Percent with College Degree",
ylab="Median Income",
main="College Degree Attainment vs. Household Income in PA",
pch=16)
points(pa.counties[pa.counties[,2]>=100,4], pa.counties[pa.counties[,2]>=100,3],
pch=17)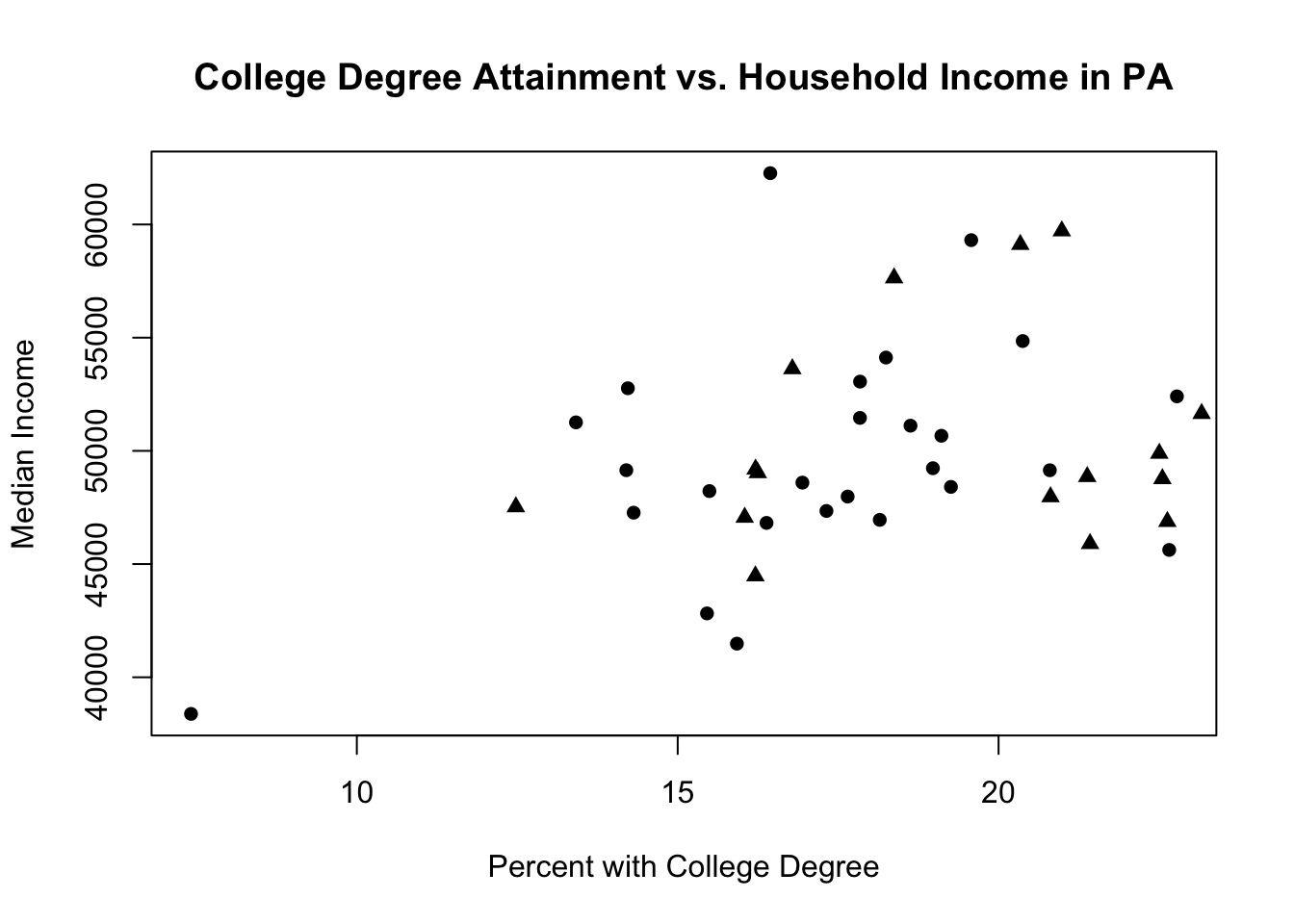
Or we could change the color:
plot(pa.counties[pa.counties[,2]<100,4], pa.counties[pa.counties[,2]<100,3],
xlab="Percent with College Degree",
ylab="Median Income",
main="College Degree Attainment vs. Household Income in PA",
pch=16,
col="forestgreen")
points(pa.counties[pa.counties[,2]>=100,4], pa.counties[pa.counties[,2]>=100,3],
pch=16,
col="darkorange")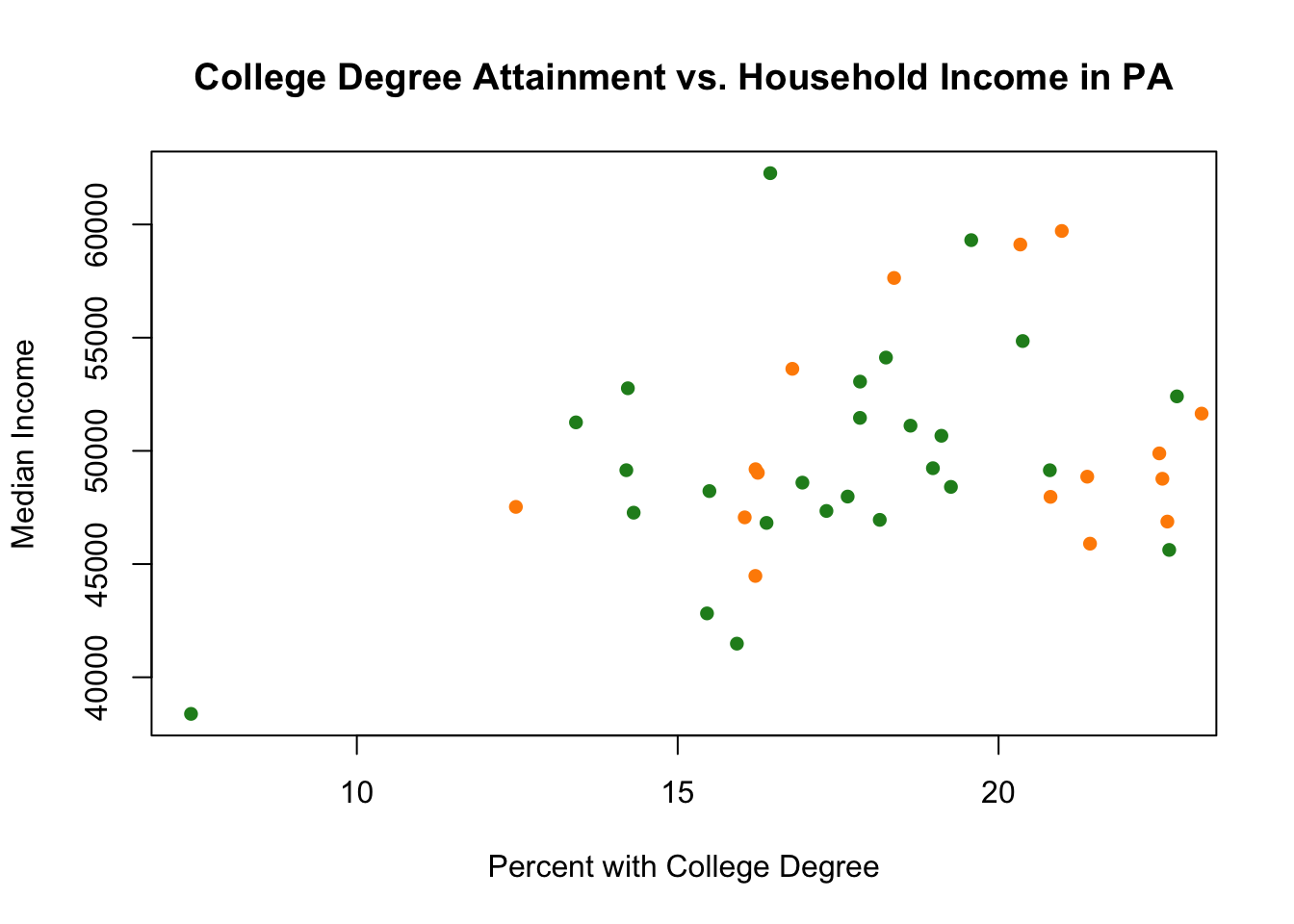
But which points are which? We can further add a legend. Again, this is a command that will generate a legend on top of an already existing figure:
plot(pa.counties[pa.counties[,2]<100,4], pa.counties[pa.counties[,2]<100,3],
xlab="Percent with College Degree",
ylab="Median Income",
main="College Degree Attainment vs. Household Income in PA",
pch=16,
col="forestgreen")
points(pa.counties[pa.counties[,2]>=100,4], pa.counties[pa.counties[,2]>=100,3],
pch=16,
col="darkorange")
legend("topleft",c("Rural","Suburban/Urban"), pch=c(16,16), col=c("forestgreen","orange"))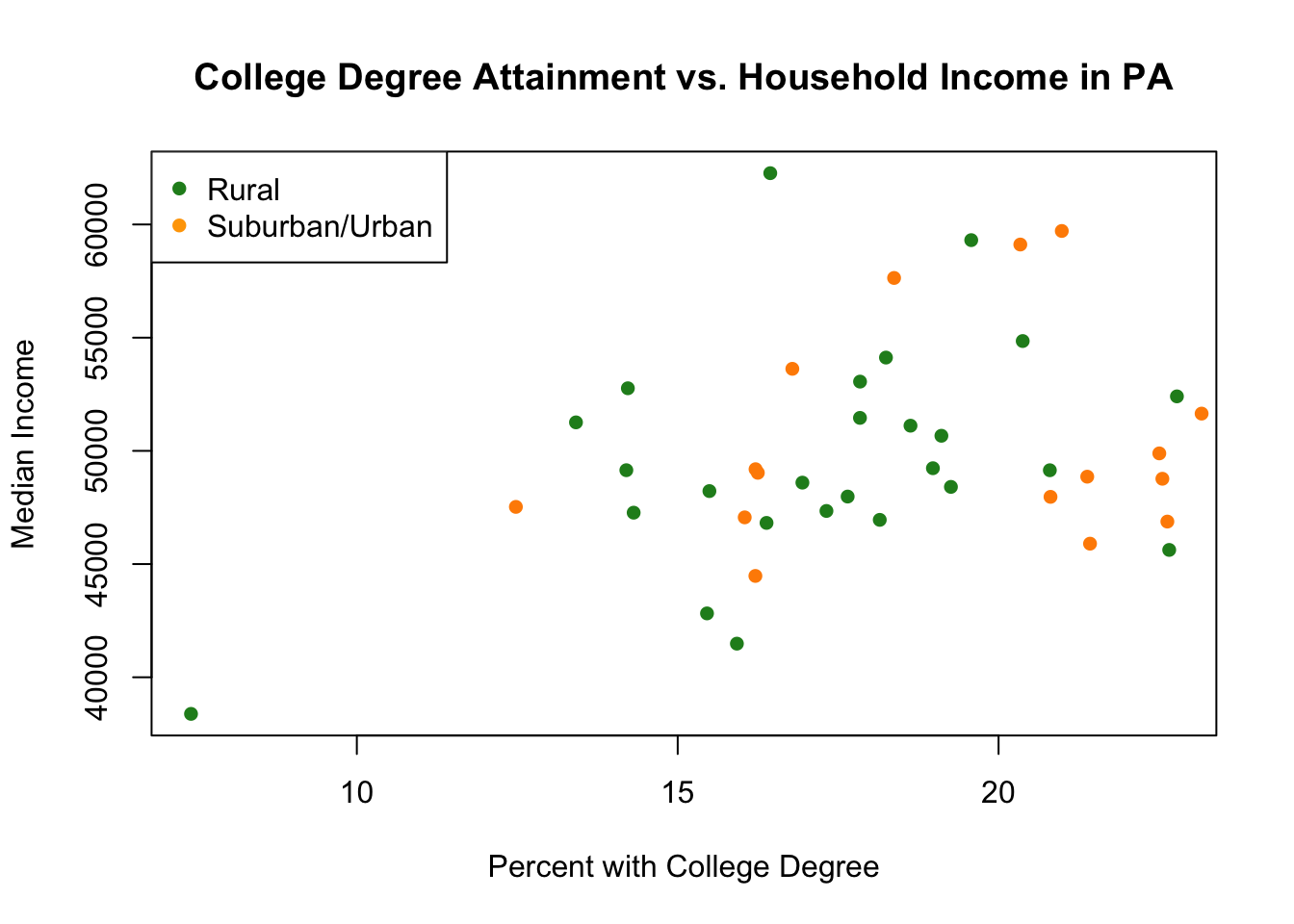
It’s hard to make a firm conclusion about my hypothesis from these data. Particularly because of the outlier we see. Can we identify that outlier?
Let’s right a boolean statement that identifies it first. For all the pa counties is the percent with a college degree less than 10?
pa.counties[,4]<10
#> [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
#> [10] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
#> [19] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
#> [28] FALSE TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
#> [37] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
#> [46] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
#> [55] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
#> [64] FALSE FALSE FALSE FALSEThere is one TRUE in there. Let’s use that to sub-set the table:
pa.counties[pa.counties[,4]<10,]
#> population population.density
#> 7.351000e+03 1.720458e+01
#> median.income percent.college
#> 3.838300e+04 7.415991e+00
#> percent.transit.commute
#> 1.187648e-01It’s that county! (We don’t have other identifyign information in this dataset right now, but we at least ID’d the row…)
One thing to be careful of when you are graphing subsets is to check the margins of the graph. You have probably noticed by now that R sets the limits of the graph to fit the range of the variables you put in the first plot() command. In the case above we let the range of median income and college among rural counties set the range for the graph. But what if that range is smaller than the range among non-rural counties?
Indeed, in this case it actually is. Look at the scales for these two graphs for rural and non-rural done separately:
plot(pa.counties[pa.counties[,2]<100,4], pa.counties[pa.counties[,2]<100,3],
xlab="Percent with College Degree",
ylab="Median Income",
main="College Degree Attainment vs. Household Income in PA (Rural)",
pch=16,
col="forestgreen")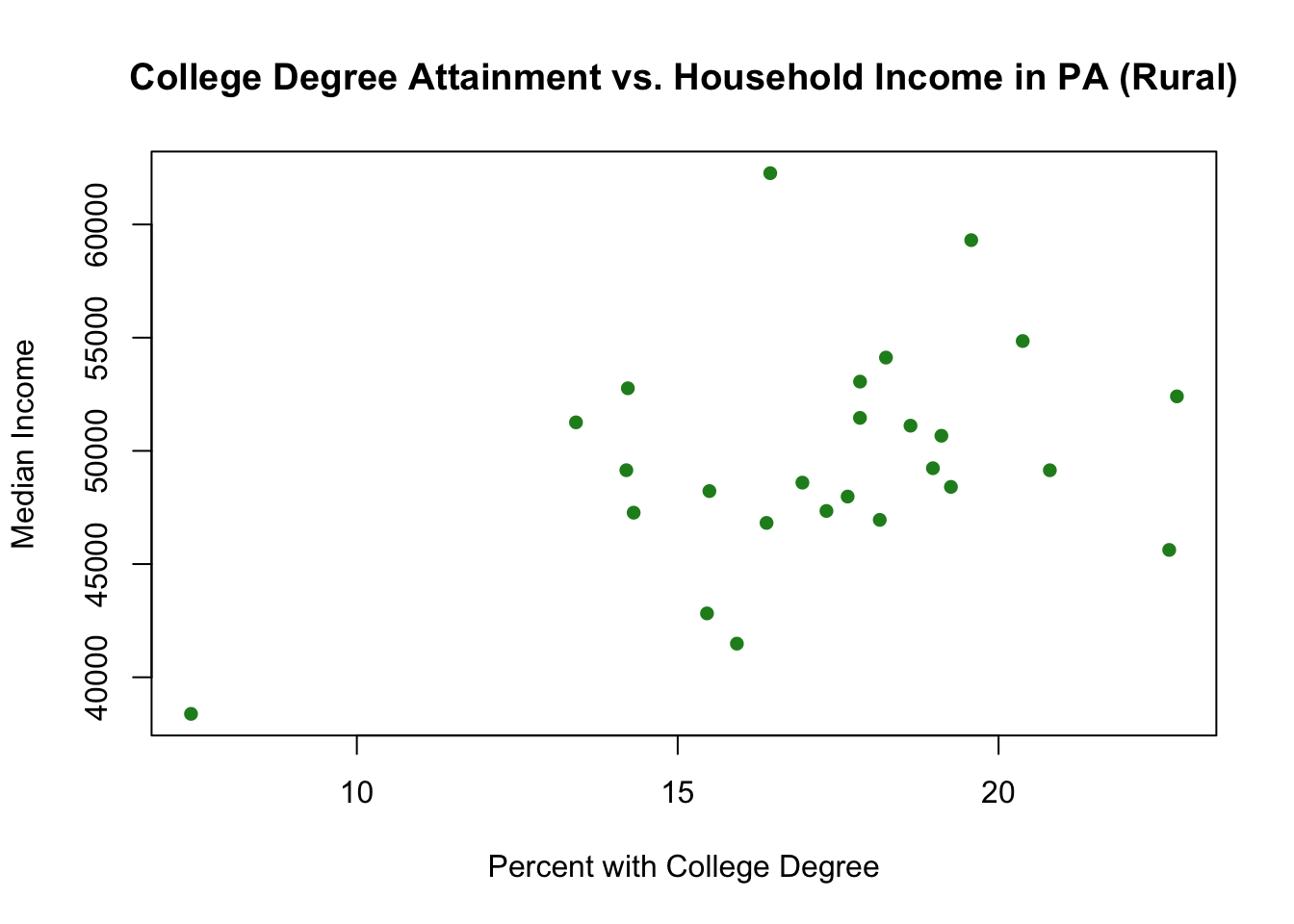
plot(pa.counties[pa.counties[,2]>=100,4], pa.counties[pa.counties[,2]>=100,3],
xlab="Percent with College Degree",
ylab="Median Income",
main="College Degree Attainment vs. Household Income in PA (Non-Rural) ",
pch=16,
col="darkorange")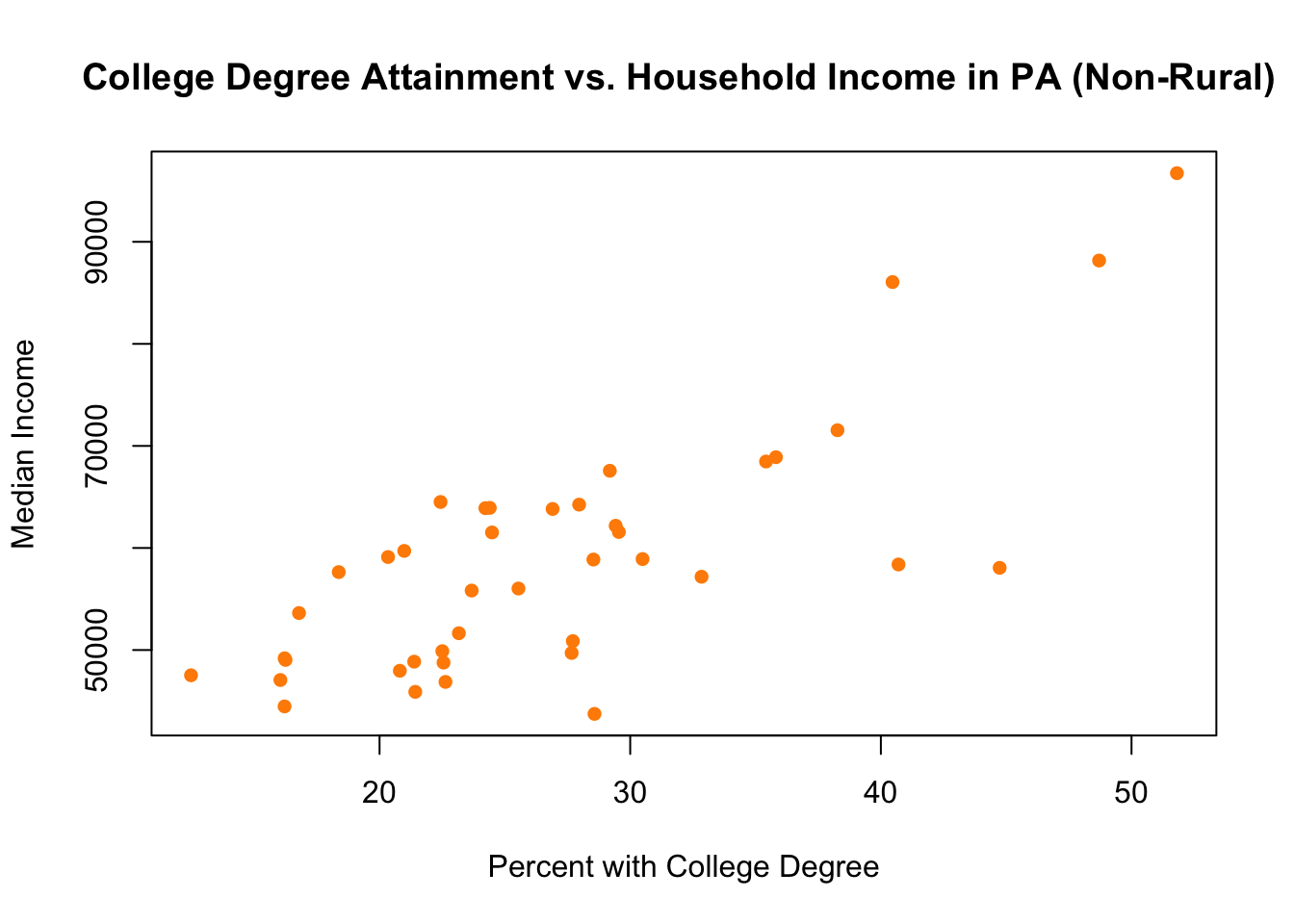
The range for the non-rural counties on both variables is way bigger! Our initial combined graph above cut off all that data. We can fix it by using xlim and ylim to manually adjust the scale of the graph:
plot(pa.counties[pa.counties[,2]<100,4], pa.counties[pa.counties[,2]<100,3],
xlab="Percent with College Degree",
ylab="Median Income",
main="College Degree Attainment vs. Household Income in PA",
pch=16,
xlim=c(0,55),
ylim=c(35000,100000),
col="forestgreen")
points(pa.counties[pa.counties[,2]>=100,4], pa.counties[pa.counties[,2]>=100,3],
pch=16,
col="darkorange")
legend("topleft",c("Rural","Suburban/Urban"), pch=c(16,16), col=c("forestgreen","orange"))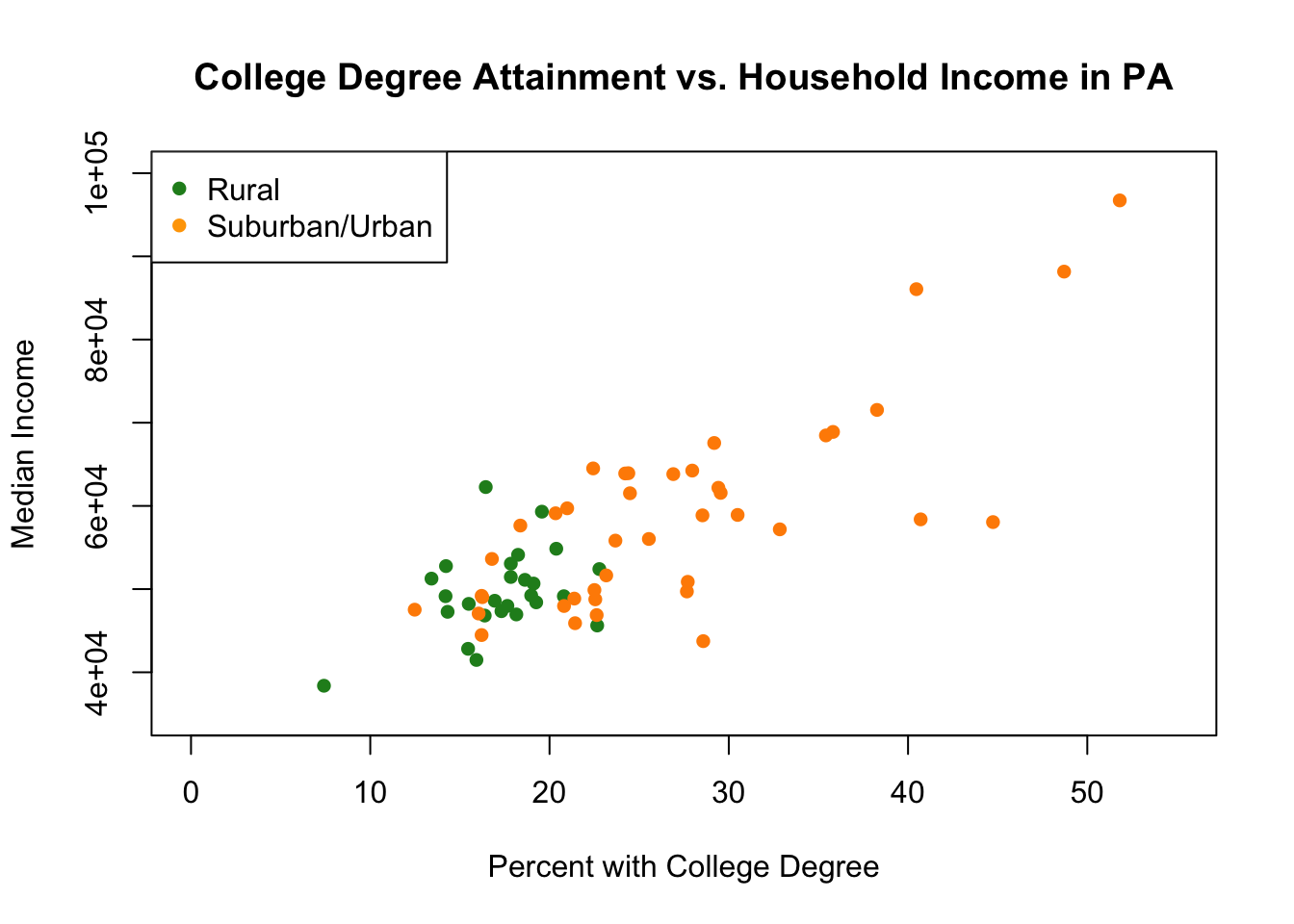
Another way that we could accomplish the same thing is to start by plotting the full relationship between the two variables using type="n" and then plotting both sets of dots on top of that empty figure:
plot(pa.counties[,4], pa.counties[,3],
xlab="Percent with College Degree",
ylab="Median Income",
main="College Degree Attainment vs. Household Income in PA",
pch=16, type="n")
points(pa.counties[pa.counties[,2]<100,4], pa.counties[pa.counties[,2]<100,3],
pch=16,
col="forestgreen")
points(pa.counties[pa.counties[,2]>=100,4], pa.counties[pa.counties[,2]>=100,3],
pch=16,
col="darkorange")
legend("topleft",c("Rural","Suburban/Urban"), pch=c(16,16), col=c("forestgreen","orange"))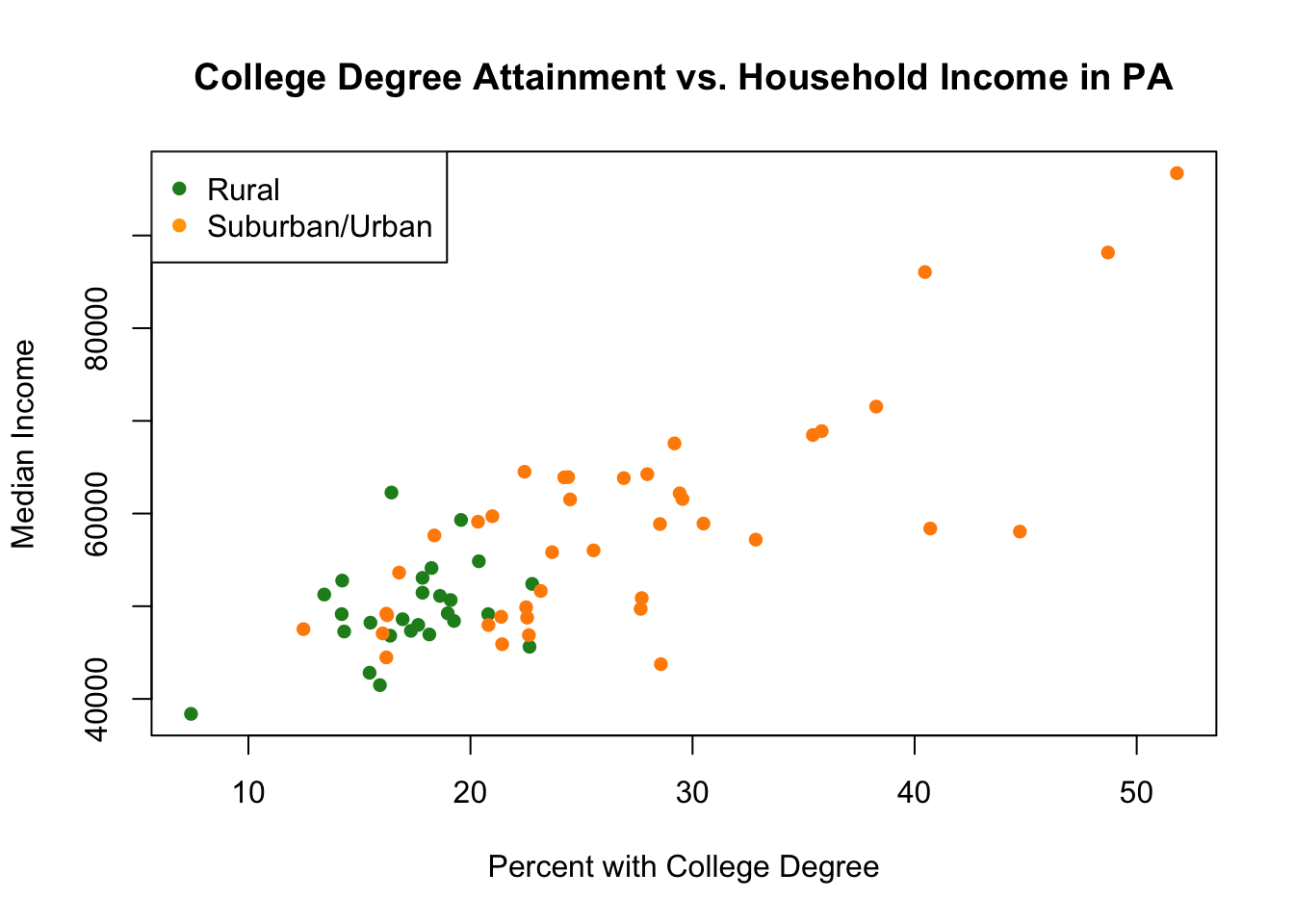
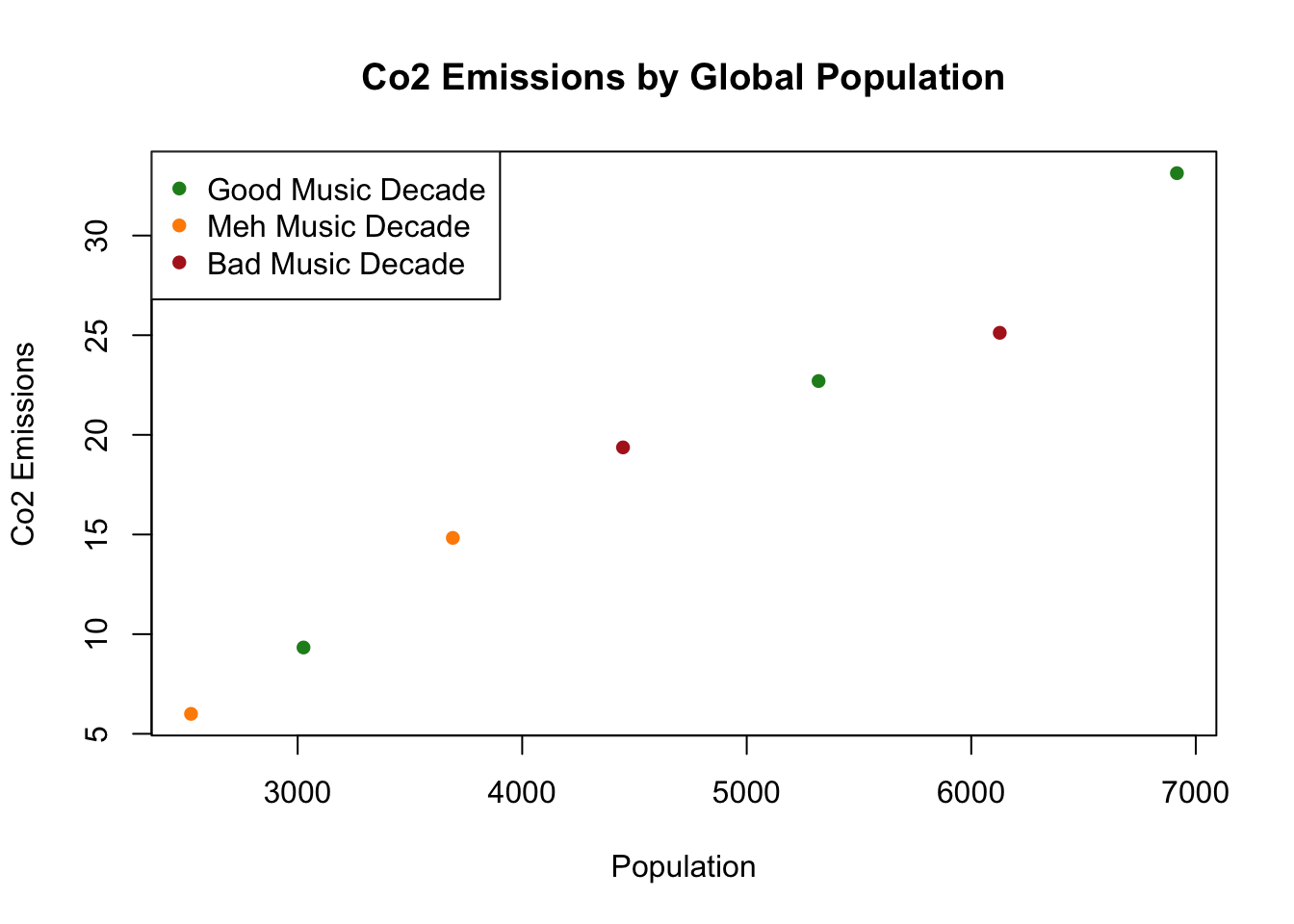
What if we wanted to make a scatterplot with pop on the x axis, and emissions on the y axis. And then color the dots according to whether the decade’s musicwas good or bad. We will then add a legend to describe what each dot color means:
plot(population.table[,2], population.table[,4], type="n",
xlab="Population",
ylab="Co2 Emissions",
main="Co2 Emissions by Global Population")
points(population.table[population.table[,5]=="good",2],
population.table[population.table[,5]=="good",4],
col="forestgreen",
pch=16)
points(population.table[population.table[,5]=="meh",2],
population.table[population.table[,5]=="meh",4],
col="darkorange",
pch=16)
points(population.table[population.table[,5]=="bad",2],
population.table[population.table[,5]=="bad",4],
col="firebrick",
pch=16)
legend("topleft", c("Good Music Decade", "Meh Music Decade", "Bad Music Decade"),
pch=c(16,16,16),
col=c("forestgreen","darkorange","firebrick"))