1 What is Data?
To produce good work in data science you need three interlocking sets of skills:
- Domain knowledge in the area you are working;
- Computational knowledge to literally process inputs and produce outputs.
- Statistical knowledge to guide decisions and to interpret findings.
My work at NBC is a good example of how these three things come together. I (and our team more broadly!) have the technical ability to write code that takes raw election returns and produces models. The models I choose and the way that I interpret them are guided by my years of experience in political science. My ability to form conclusions based on the data I am seeing is based on my knowledge of mathematical statistics. All three of these things have to work in concert for me to be a good analyst.
This course is primarily going to focus on (2). And there is a lot to focus on there! Learning how to use R to load, merge and clean data is hard! As is using R to generate output and figures. That is definitely a course-worth of material.
But it’s important to remember that this is only one leg of a three-legged stool.
Domain knowledge you are going to get in your other classes and through your life experience. Whether it’s politics, business, sports, economics… Over time you will gain knowledge of theories that guide behavior in those fields, learn what is important to people etc.
Statistics knowledge will take a specific investment from you to improve. And I highly recommend you make that investment. Even if you have already taken AP stats, it is incredibly helpful to re-learn the basics of statistics at the college level. (Seriously, it is hard to spend too much time on the basics).
The purpose of today’s lesson is to give you an intuitive and non-mathematical introduction to what “statistics” is. This is something for you to keep in mind as we spend time building your technical skills in this class.
1.1 Why isn’t this class “statistics”?
In this class we are going to be working with data, making tables and figures, generating values like the mean, or median… by all normal definitions this is “statistics”. But it’s not, really.
Statistics is the science of inferring facts about the real world from samples of data.
Ok, but why is that hard? And why does that have to be a whole science on to itself?
To understand this, let’s take on a pretty classic statistics question: using a public opinion poll to predict who is going to win an election.
We are going to look at the 2022 Senate election in Pennsylvania won by John Fetterman over Mehmet Oz. At the end of this lecture we will look at some real data on this question, but for right now we are going to invent some data.
Say we want to understand who is going to win the election so we go out and poll 100 randomly selected Pennsylvanians. You don’t need to know the details here, but I am drawing this sample from the “truth” of the real election result: Fetterman won 52.5% of the voters who voted for either him or Oz. We get the following data back:
set.seed(2)
support.fetterman.prime <- rbinom(100,1, .525)
head(support.fetterman.prime,10)
#> [1] 1 0 0 1 0 0 1 0 1 0We have 100 observations of 0s and 1s here, where 1 indicates the individual supports John Fetterman and 0 indicates the individual supports Mehmet Oz.
We are going to use this type of variable, an “indicator” variable a lot. They are very helpful because if you take the mean of a bunch of 1s and 0s you get the proportion of time the variable is a 1. In this case, this gives us the proportion of people in this poll who support Fetterman over Oz:
mean(support.fetterman.prime)
#> [1] 0.57In this poll 57% of people supprt John Fetterman.
So if we saw this poll in October 2022, would we confidently declare that Fetterman is going to win?
The problem – and here’s where we get to why this class isn’t statistics – is that this is just one sample of 100 Pennsylvanians out of an infinite number of possible samples of 100 Pennsylvanians. We have no interest in simply describing what is happening with these 100 Pennsylvanians, we want to know what’s happening with all Pennsylvanians.
But how do we know that this sample is a good sample? Maybe this is just a weird group of people! Fetterman did, indeed, win this election (though, not by this much), but we would not have known that at the time!
For example, here is another sample of 100 people drawn from the same underlying truth:
In this poll 46% support Fetterman and 54% support Oz. So the opposite result! Which of these two polls is right?
Let’s grab 10 polls of 100 people to see what kind of range we are looking at:
set.seed(4)
fett.polls <- NA
for(i in 1:10){
support.fetterman <- rbinom(100,1, .525)
fett.polls[i] <- mean(support.fetterman)
}
sort(fett.polls)
#> [1] 0.46 0.47 0.51 0.54 0.55 0.55 0.58 0.59 0.60 0.66So in these 10 polls we have a range of 20 percentage points!
So let’s think systematically about this. Here is a visual representation of our original poll result, relative to 50%:
plot(c(.3,.7), c(0,10), type="n")
abline(v=.5, lty=3, lwd=2)
abline(v=mean(support.fetterman.prime), col="firebrick", lty=2)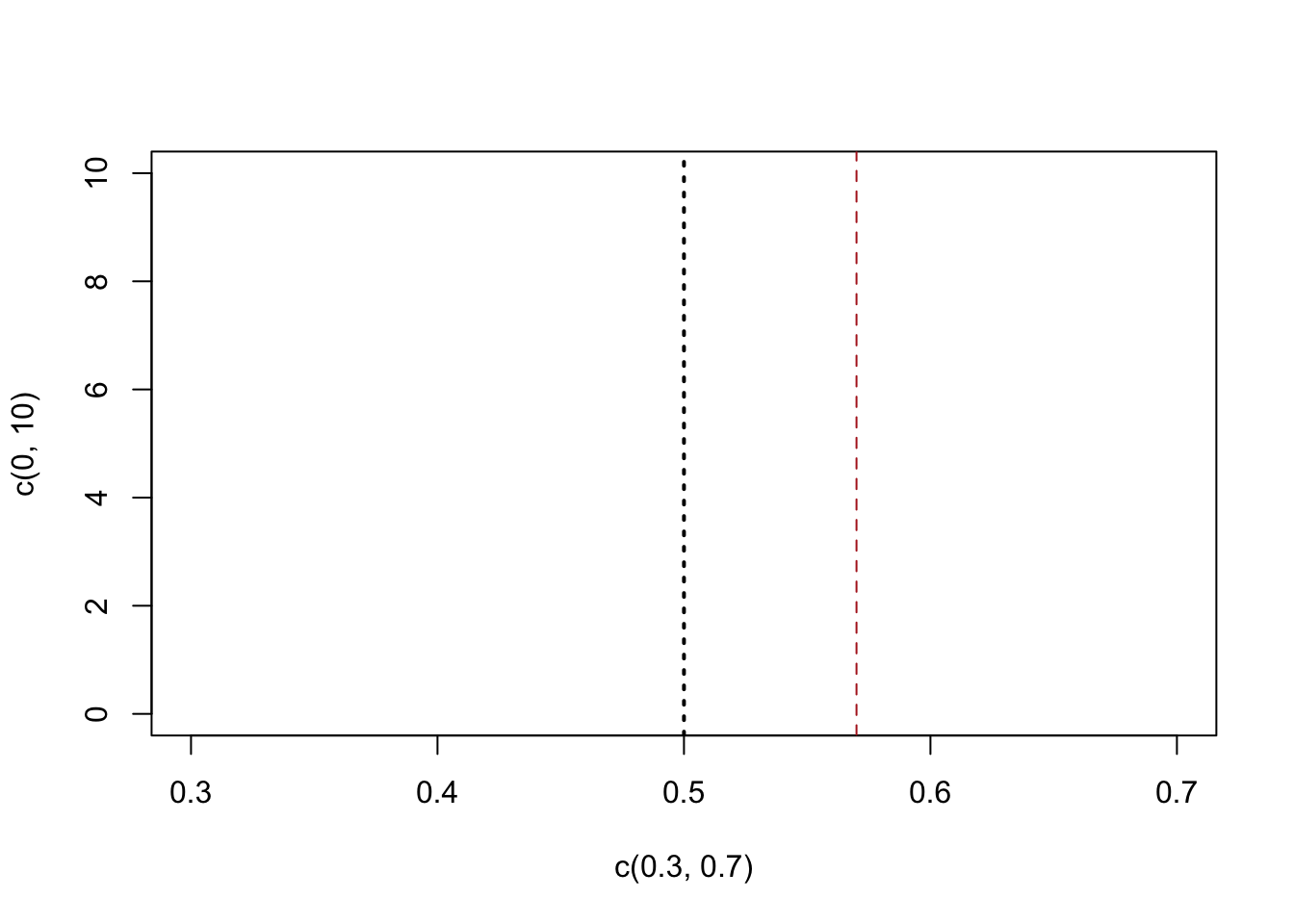
The problem we are facing is this. We only get this one poll, and we want to make a conclusion about the broader truth about the degree to which Pennsylvanians support Fetterman. We know that if we take other samples of 100 we will get different answers. So what do we do?
Here’s how we think about this like a statistician: if the truth is that the race is tied, would that make our result surprising?
We’ve seen that different sample of 100 people will give a range of different answers. What we do in statistics is systemically estimate that noise, and then determine if our result is plausible or not given that noise and an assumption about the truth.
We will get to the systematic answer shortly, but for right now we can use the fact that we’ve generated 10 different samples of 100 people and found that the range was 20 percentage points to try to visualize this idea:
plot(c(.3,.7), c(0,10), type="n")
abline(v=.5, lty=3, lwd=2)
abline(v=mean(support.fetterman.prime), col="firebrick", lty=2)
arrows(.4,5, .6, 5, col="dodgerblue", code=3)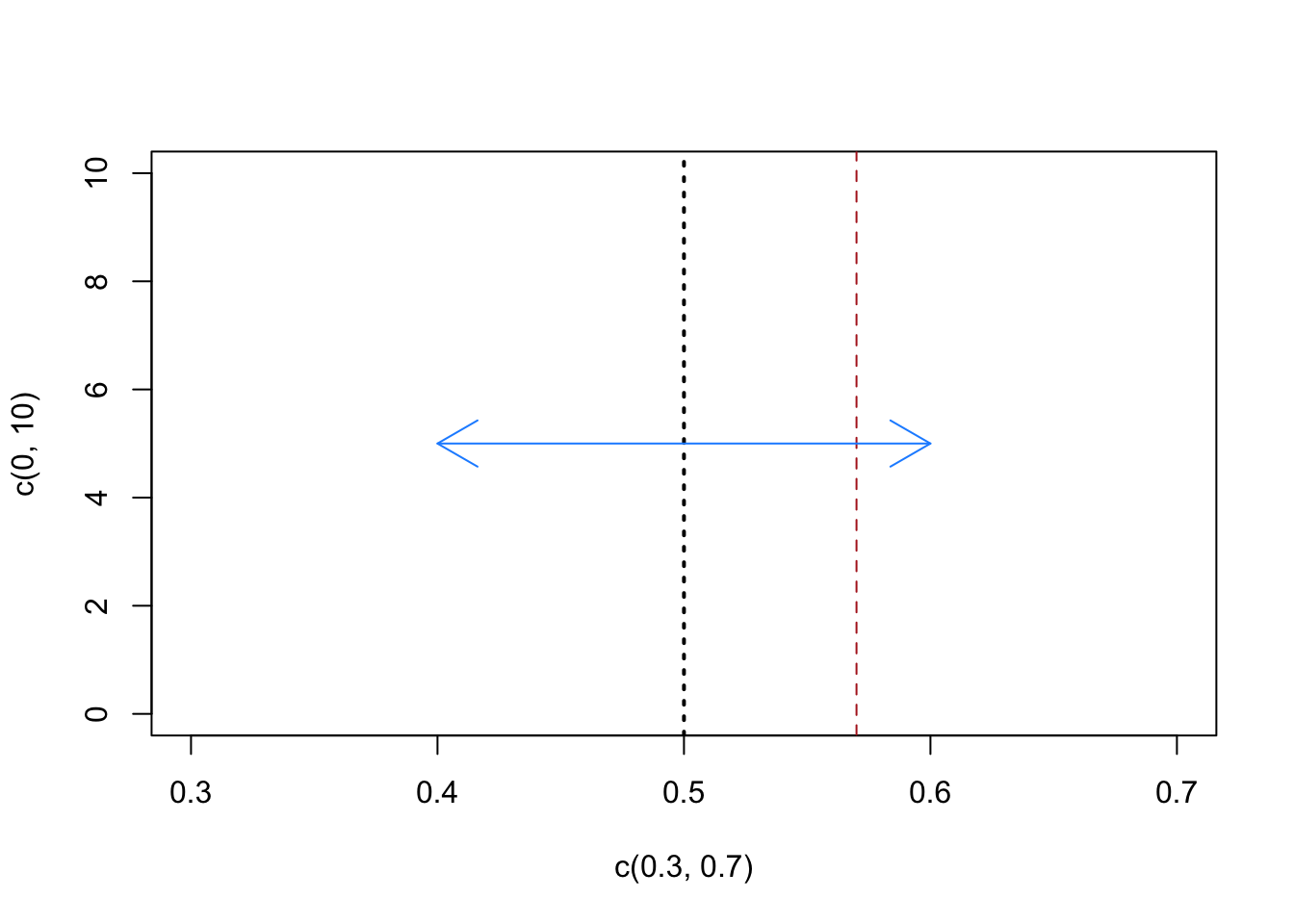
We have our original estimate in red, and centered on the all-important 50% (the race is tied!) we have our current guess of the range of possibilities (plus or minus 10 points). So: given our current guess of the range of possibilities due to random sampling, does the red line seem special? I would answer no right now, the amount of variability due to random sampling we have seen is such that I can’t rule out that the truth is 50%.
What we want to understand in statistics is how big to make the blue bar in the graph above. How much random variation is possible and, therefore, does our particular result stand out relative to some benchmark value?
1.2 Coin Flip Modelling
This type of thinking is a bit easier when we have a clear model for the underlying uncertainty/noise. In particular, when we think of events that can be modeled as a “coin flip” we can easily measure the underlying uncertainty in outcomes.
Say I present you with a coin, and I want you to determine if it’s a “fair” coin or not. That is: is this a coin that we expect to come up heads 50% of the time and tails 50% of the time?
You flip the coin 10 times and you get the following sequence, where 1 represents heads and 0 represents tails:
c(0,1,1,1,0,1,1,0,1,1)
#> [1] 0 1 1 1 0 1 1 0 1 17 heads and 3 tails. This seems like a lot of heads!
But as above, we know that every time we flip 10 coins we are going to get a slightly different answer. Again, we want to make a measurement of this uncertainty and determine if our particular case is special, or not.
Here we are trying to answer the question: what if this coin is fair? So what if this coin is fair?? We can just simulate flipping a fair coin 10 times a whole bunch of times and determine the range of outcomes. Here is R code that flips a fair coin 10 times:
Let’s just do that a whole bunch of times and determine the range of possibilities that might occur in terms of the number of heads:
num.heads <- NA
for(i in 1:10000){
num.heads[i] <- sum(sample(coin, 10, replace=T))
}
head(num.heads,10)
#> [1] 5 5 3 6 3 6 2 6 6 5We have 10,000 samples of 10 flips of a coin. This allows us to visualize: what outcomes are likely and un-likey when a fair coin is flipped 10 times.
cols <- c(rep("gray",7), "firebrick", rep("gray", 3))
barplot(prop.table(table(num.heads)), col=cols)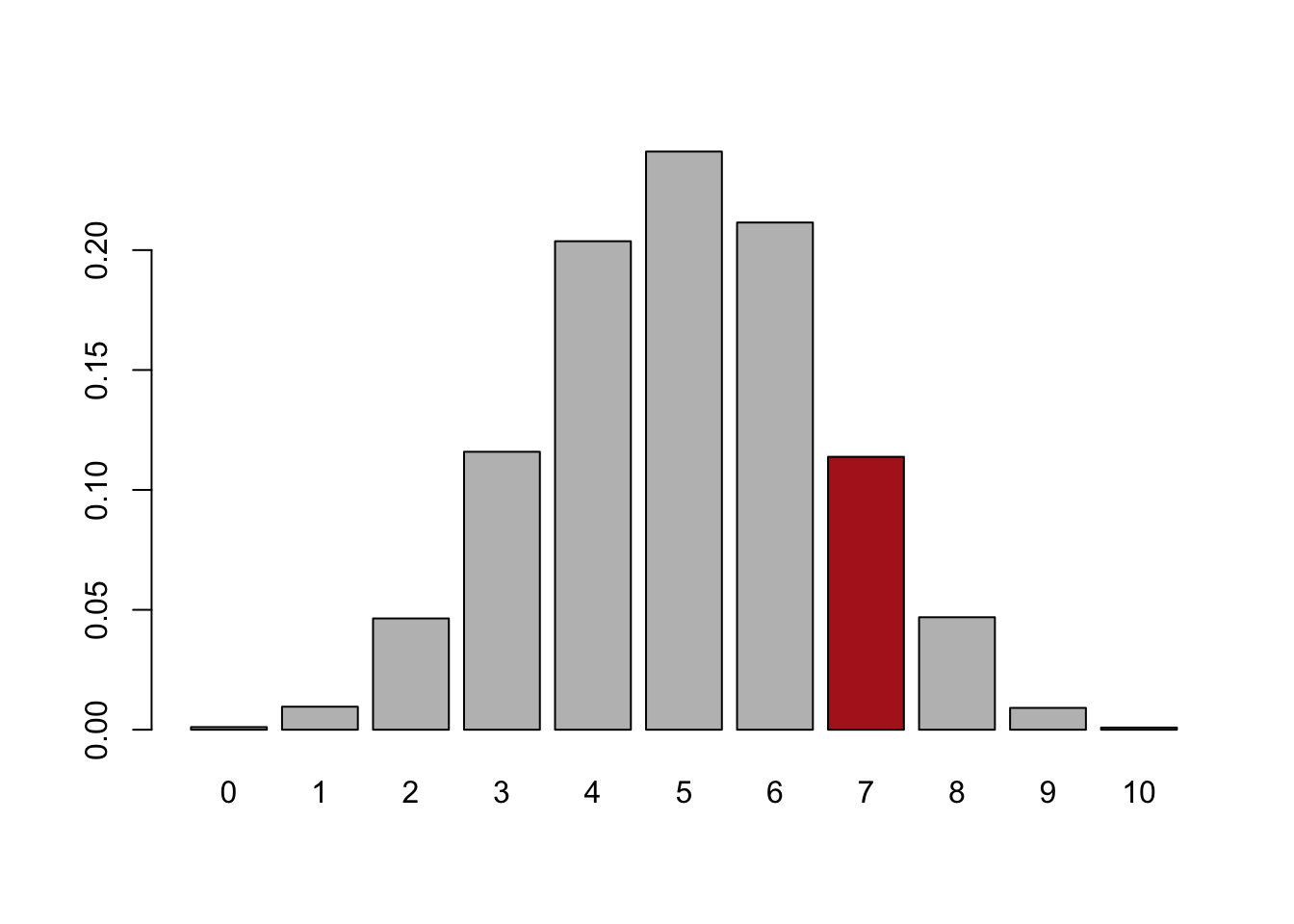
Above is a histogram of what happens when you flip a fair coin 10 times. Of course, the most likely thing to happen is that you get exactly 5/10 heads. Getting 4 or 6 heads is still quite likely. You pretty much never get 0 or 10 heads. This graph is describing the random sample variation that occurs when flipping a coin.
In red is our original observation, getting 7 heads in 10 flip of the coin. We see that this occurs about 12% of the time when flipping a fair coin. 12% is pretty rare, I wouldn’t bet my house on it, but it is a pretty frequent occurence. From that, I don’t think we can overturn the idea that the coin we are flipping is a fair coin.
What if we had got 9 heads in 10 flips?
cols <- c(rep("gray",9), "firebrick", rep("gray", 1))
barplot(prop.table(table(num.heads)), col=cols)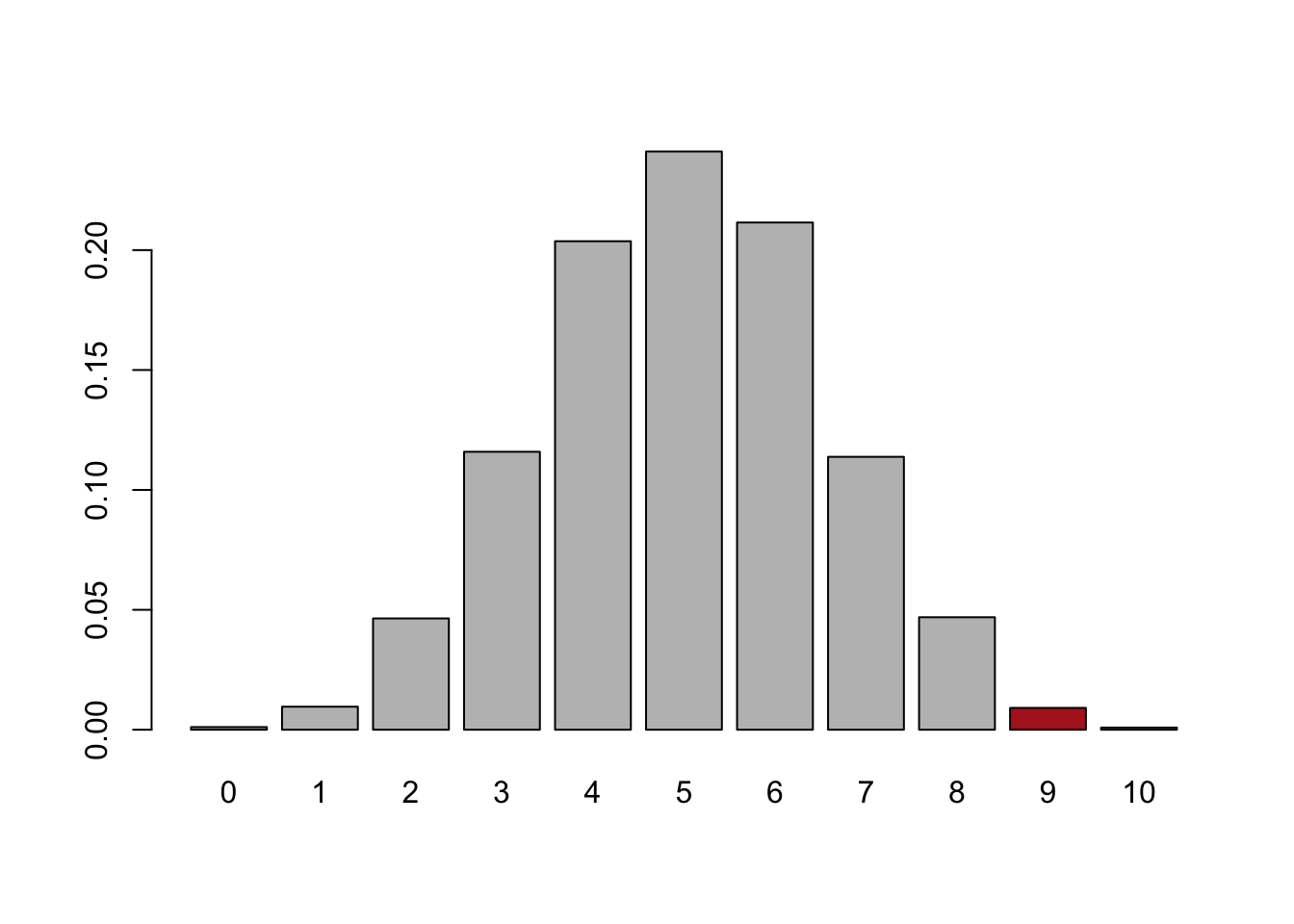
This happens very rarely, around 2% of the time. If that was what had happened, we would be much more comfortable saying: no, this is very likely not a fair coin.
How can we apply this type of coin-flip modeling to a real world example?
In the excerpt from the Drunkard’s Walk posted on canvas, Mlodinow goes through several examples of situations where signal cannot be discerned from noise: the record of fighter pilots, baseball players, and movie producers. In all of these situations, people were able to tell extraordinarily convincing and logically coherent stories about why they were witnessing the signal, but in all the cases they were just seeing random noise. Statistics is important because it can help us tell the difference between these two things.
Let’s expand on Mlodinow’s example of the movie producer, Shelly Lansing.
At the start of Lansing’s tenure as an executive she produced three hit movies: Forest Grump, Braveheart, and Titanic. Three movies that even you young people have heard of and have probably seen. Except Braveheart. That really hasn’t aged well. You don’t need to go see Braveheart.
But after that she produced four dud films including Timeline, and Tomb Raider: The Cradle of Life. You have not head of these movies, and you almost certainly have not seen these movies.
The “story” that her bosses told themselves is that Lansing’s performance had declined. She had started to play it safe, and playing to “middle of the road” tastes. She was no longer taking big risks.
What can we do to sort through this?
Like above, we can treat this as a “coin flip” model. If we start with the proposition that movie produces have no ability to pick winners and losers, we can model out what range of random outcomes will occur. This is just like a coin being flipped heads and tails. We want to know if getting only 3 wins in 7 movies is special. To do so we can generate more examples of what 7-movie stretches would look like:
Just like above, we see that if we repeat the sampling process we get something slightly different every time.
To get a sense of how much random variation there are in 7 flips of a coin, I’m going to repeat this sampling process many, many, times. Each time I’m going to record how many Ws there are.
number.wins <- NA
for(i in 1:10000){
number.wins[i] <- sum(sample(c("W","L"), 7, replace=T)=="W")
}
table(number.wins)
#> number.wins
#> 0 1 2 3 4 5 6 7
#> 71 562 1604 2720 2757 1649 557 80
cols <- c("gray", "gray", "gray", "firebrick", "gray","gray",
"gray", "gray")
barplot(table(number.wins), col=cols)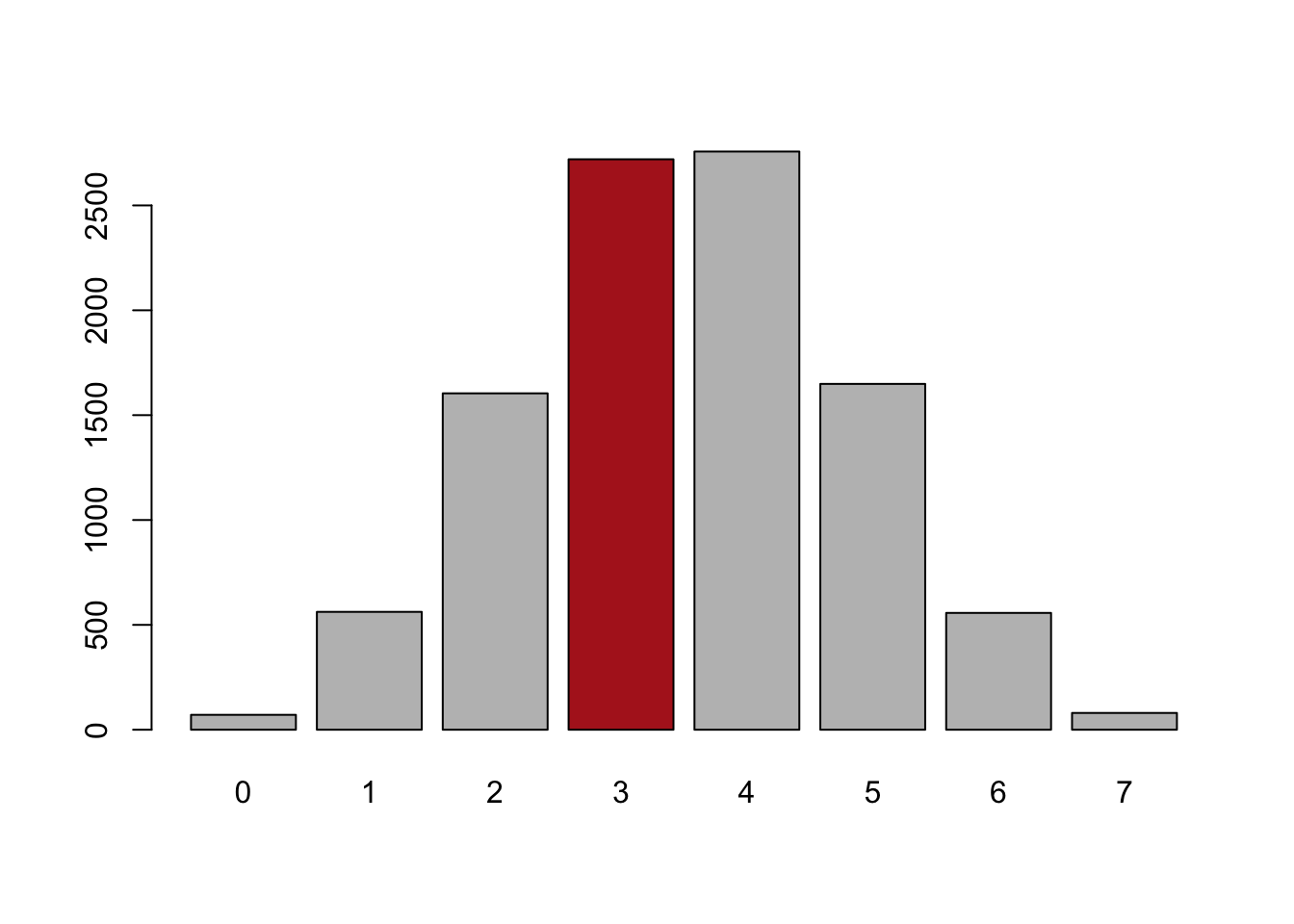
We see that our repeated sampling from a world where wins and losses are equally likely that we get 3 wins in 7 films pretty frequently, approximately 25% of the time. Using the logic above: if the truth is that movie producers have no ability to pick winners and losers, we would expect to see someone get 3 wins in 4 losses relatively frequently, around 25% of the time. Because of that, when we observe Lansings 7-movie run, we can’t distinguish it from what would happen just by random chance.
As a sidebar: you might complain that what we really want to look at is the odds of having a streak of 4 losses in 7 movies instead of just 4 losses. Here is that code:
streak <- NA
for(i in 1:10000){
x <- sample(c("W","L"), 7, replace=T)
x
out <- rle(x)
out$lengths <- out$lengths[out$values=="L"]
streak[i]<- any(out$lengths>4)
}
prop.table(table(streak))
#> streak
#> FALSE TRUE
#> 0.9374 0.0626That happens around 6% of the time. Slightly more rare!
What would allow us to actually make a firm conclusion about a move producer’s level of talent?
Let’s say we allowed Lansing to have a long (an absurdly long) career and allowed her to make 70 movies. Further, let’s imagine that in those 70 movies she has 30 hits. Notice that this is exactly the same proportion of “hits” as she got in the real world! But now the totals are scaled up.
Without thinking about math, would we be more or less confident that Lansing is a “bad” producer given this new information? My intuition is that we should be more confident at this point. We have more information that is consistent with her having more losses than wins at the box office.
We can modify the above code to look at what we can expect if wins and losses were just random, but instead look at 70 movies:
sample(c("W","L"), 70, replace=T)
#> [1] "W" "L" "W" "L" "L" "L" "W" "L" "L" "W" "W" "L" "W" "L"
#> [15] "L" "L" "W" "L" "L" "W" "W" "L" "W" "L" "L" "L" "W" "L"
#> [29] "W" "L" "W" "L" "W" "L" "L" "L" "W" "L" "W" "W" "L" "L"
#> [43] "L" "L" "L" "L" "L" "W" "W" "W" "W" "L" "L" "L" "W" "L"
#> [57] "W" "W" "W" "W" "L" "L" "L" "L" "W" "L" "L" "L" "W" "W"Again, to understand if 30 wins in 70 movies is “surprising” if producers have no ability to pick winners and losers, we need to understand the randomness that is inherent when sampling 70 movies. If producers have no ability to pick winners and losers, that’s just like a 50/50 coin, so we can model this uncertainty by flipping a coin 70 times a large number times and looking at the resulting distribution:
number.wins <- NA
for(i in 1:10000){
number.wins[i] <- sum(sample(c("W","L"), 70, replace=T)=="W")
}
table(number.wins)
#> number.wins
#> 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
#> 1 3 6 19 36 61 91 169 236 345 485 632 741 848 938
#> 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49
#> 891 917 821 766 580 493 332 226 157 99 44 30 15 11 4
#> 50
#> 3
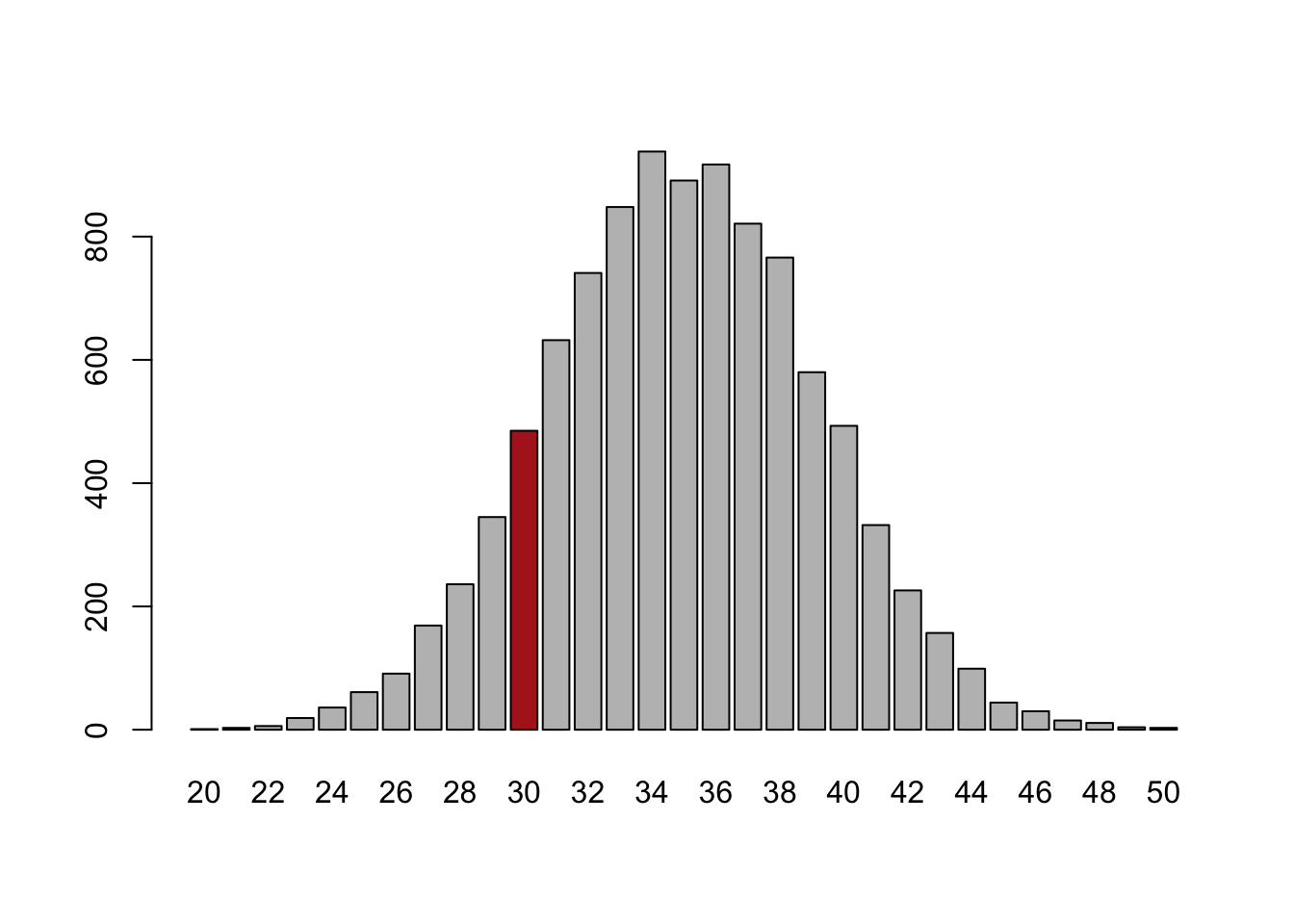
Before, we saw that by random choice we could expect to get 3 wins in 7 films around 25% of the time. But looking at this simulation we get 30 wins in 70 films a smaller amount of the time, now around 5% of the time.
Even though the deviation from 50% is the same here, with more observations we are more confident that this deviation is meaningful. Put another way: in 7 flips of the coin it’s not weird at all to get 3 heads; with 70 flips of the coin it’s somewhat weird to only get 30 heads. Taken to the extreme, it would be extremely weird to get only 3000 heads in 7000 flips of a coin:
number.wins <- NA
for(i in 1:10000){
number.wins[i] <- sum(sample(c("W","L"), 7000, replace=T)=="W")
}
barplot(table(number.wins))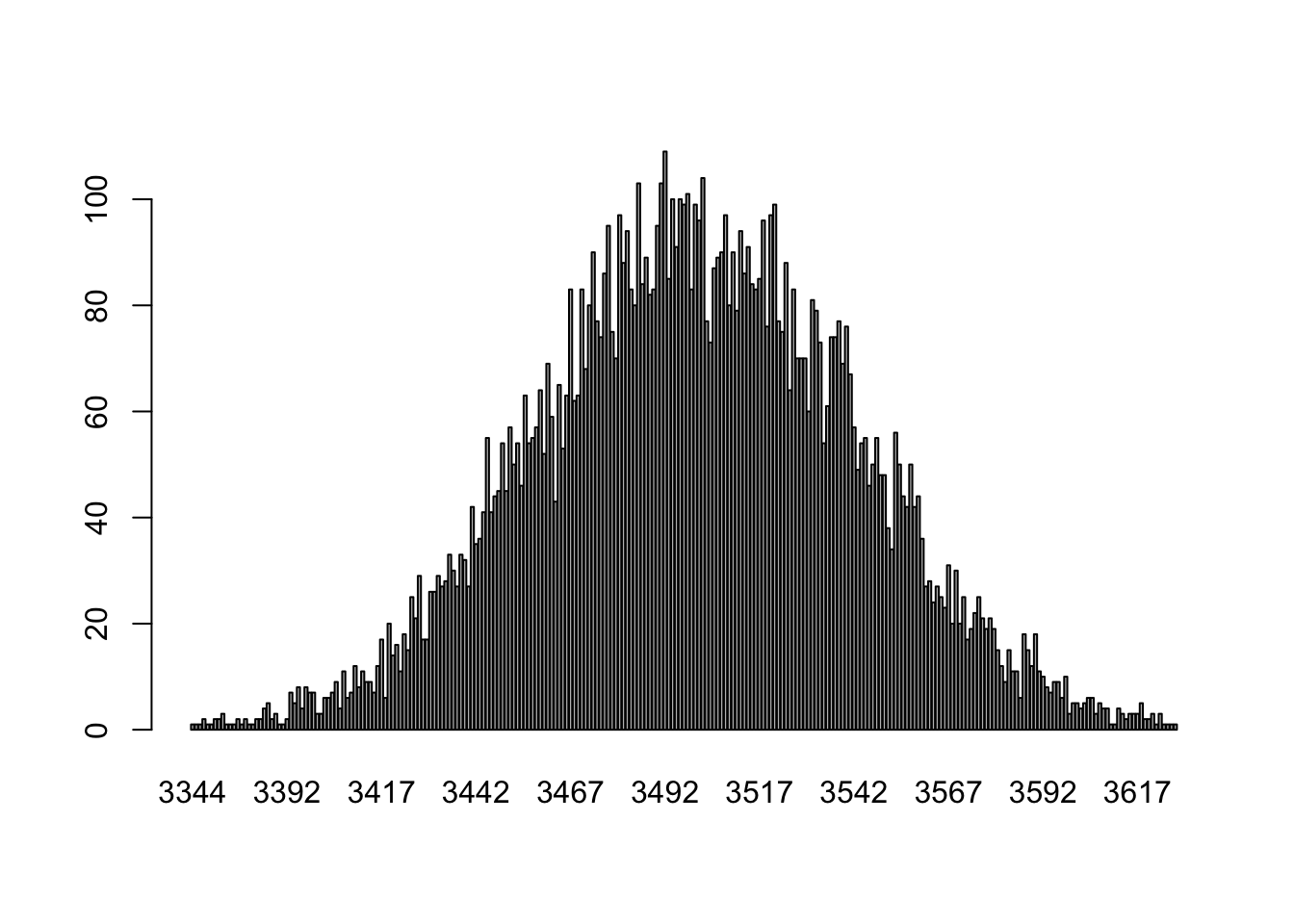
3000 is not even on this graph.
The amount of random fluctuation we see from sampling is not a fixed thing. The more observations we have, the more a particular deviation from the expected average will stand out.
1.3 Back to the real world
So in some situations we can model the underlying uncertainty really easily and compare what we have observed what is likely to happen simply due to random chance. How does that help us in the real world when have a dataset like we had at the start of the lecture?
Indeed, here is the real data:
pa.dat <- rio::import("https://raw.githubusercontent.com/marctrussler/IIS-Data/refs/heads/main/PAFinalWeeks.csv")
pa.dat <- pa.dat[!is.na(pa.dat$senate.topline) & pa.dat$senate.topline!="Other/Would not Vote",]
pa.dat$vote.fet <- pa.dat$senate.topline=="Democrat"
nrow(pa.dat)
#> [1] 4369
mean(pa.dat$vote.fet, na.rm=T)
#> [1] 0.5566491This is data on 4369 real Pennsylvanians on how they are going to vote in the election. In this group 55.6% say they are going to vote for Fetterman.
We know that if we went out and got another sample of 4369 people we are not going to get the same answer. We have learned that the correct way to go about this is to say: what if they truth is that the race is tied, can we build a model of the amount of uncertainty that we could expect for a sample of this size, and see if our result seems special relative to the expected noise?
Above we used simple coin flips to determine the degree to which an event is special, and indeed, in this particular case we can do the same thing. If people are ambiguous about Oz and Fetterman we can imagine each of the 4369 people flipping a coin to provider their answer to the survey. If this is what is happening, how likely would it be that 2429 (55.6%) of them say they are going to support Fetterman?
vote.fetterman<- NA
for(i in 1:10000){
vote.fetterman[i] <- sum(sample(c("Fetterman","Oz"), 4369, replace=T)=="Fetterman")
}
barplot(table(vote.fetterman))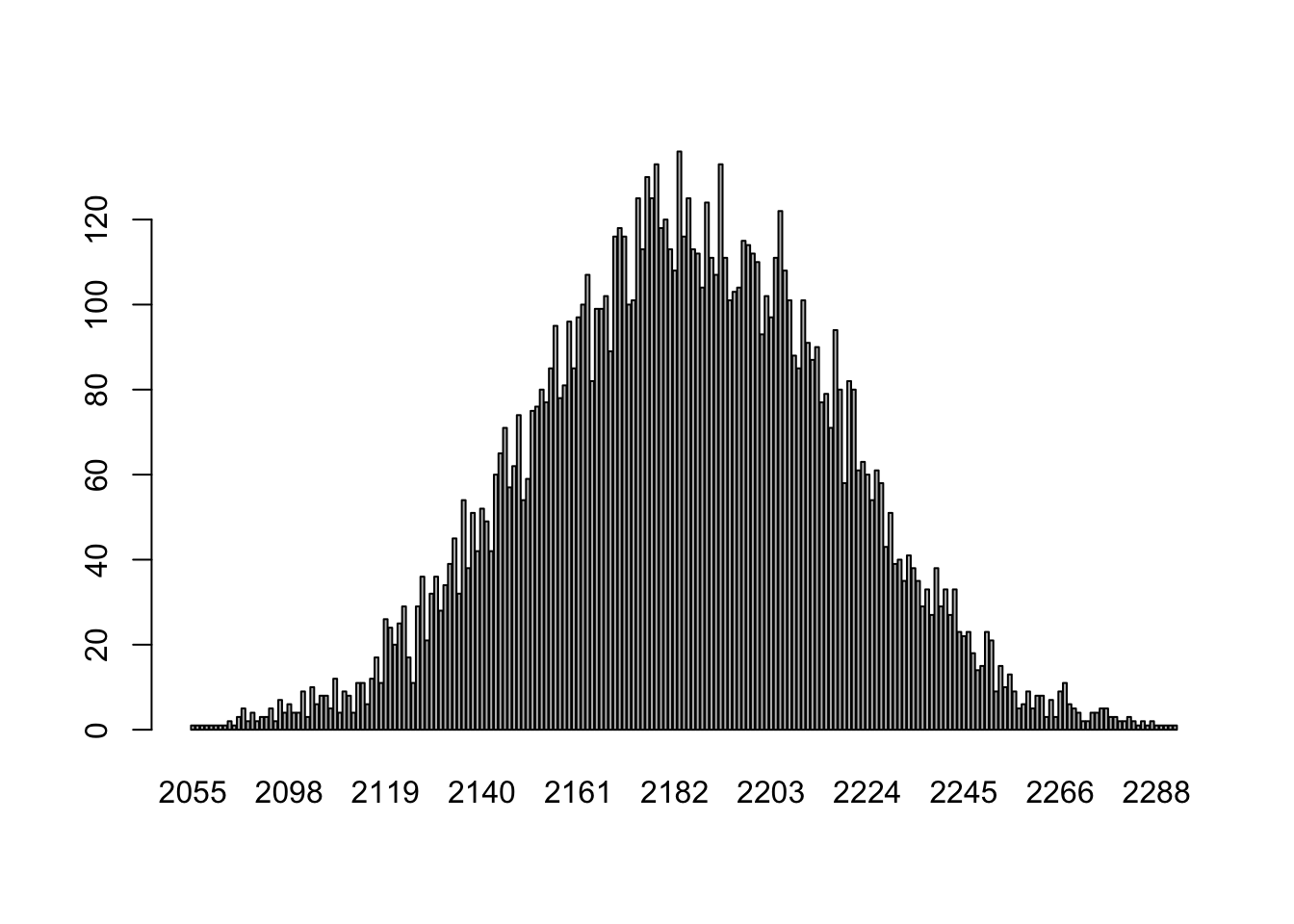
When we flip 4369 coins these are the outcomes that occur at different probabilities. Again: 2429 is not even in this chart. In other words: if we treat each survey respondent as if they are a 50/50 coin, it is nearly impossible for us to see the result that we saw (2429 supporting Fetterman). We can reject the idea that this race is tied.
But not everything can be modeled like a coin flip. What if we wanted to know the average ideology of Pennsylvanians? Where ideology is measures on a 5 point scale from “Very liberal” (1) to “Very Conservative” (5)?
table(pa.dat$ideology)
#>
#> Conservative Liberal Moderate
#> 1132 809 1651
#> Very conservative Very liberal
#> 396 363
pa.dat$ideo5[pa.dat$ideology=="Very liberal"] <- 1
pa.dat$ideo5[pa.dat$ideology=="Liberal"] <- 2
pa.dat$ideo5[pa.dat$ideology=="Moderate"] <- 3
pa.dat$ideo5[pa.dat$ideology=="Conservative"] <- 4
pa.dat$ideo5[pa.dat$ideology=="Very conservative"] <- 5
mean(pa.dat$ideo5,na.rm=T)
#> [1] 3.089405In our sample the average respondent has an ideology of 3.1, or just right of the “moderate” point of 3.
Now using the logic we have used so far, we can ask: if the true average ideology of Pennsylvanians is “moderate” (3), what are the odds that I would get 3.1 in a sample of 4369 people?
But in this case, we can’t just pretend that people are flipping a coin. Even if we modeled it as a 5 sided dice that people rolled that would be making an assumption that being Very Liberal was just as likely as Very Conservative. And what if instead we were interested in a continuous variable, something like height?
Instead we turn to math. The full derivation of this can wait until 1801, but for now we can express this concept of “how much noise can we expect there to be due to sampling” as the standard error. For a single mean, we can get the standard error through this formula:
\[ \frac{sd(x)}{\sqrt{n}} \]
The standard error is calculated by dividing the standard deviation of what we have a sample of and dividing by square root of the sample size.
So, in this example, we can take the standard deviation of ideology and divide by the square root of 4369:
Every time we sample 4369 people and ask about their ideology we will get a little bit different answer. The amount that these same ideologies will differ from the truth ideology of Pennsylvanians is 0.016. We can visualize that like this
eval <- seq(2.75,3.25,.001)
plot(c(2.75,3.25), c(0,25), type="n")
points(eval, dnorm(eval, mean=3, sd = se), type="l", col="dodgerblue")
abline(v=3, lty=3, lwd=2)
abline(v=mean(pa.dat$ideo5,na.rm=T), col="firebrick", lty=2)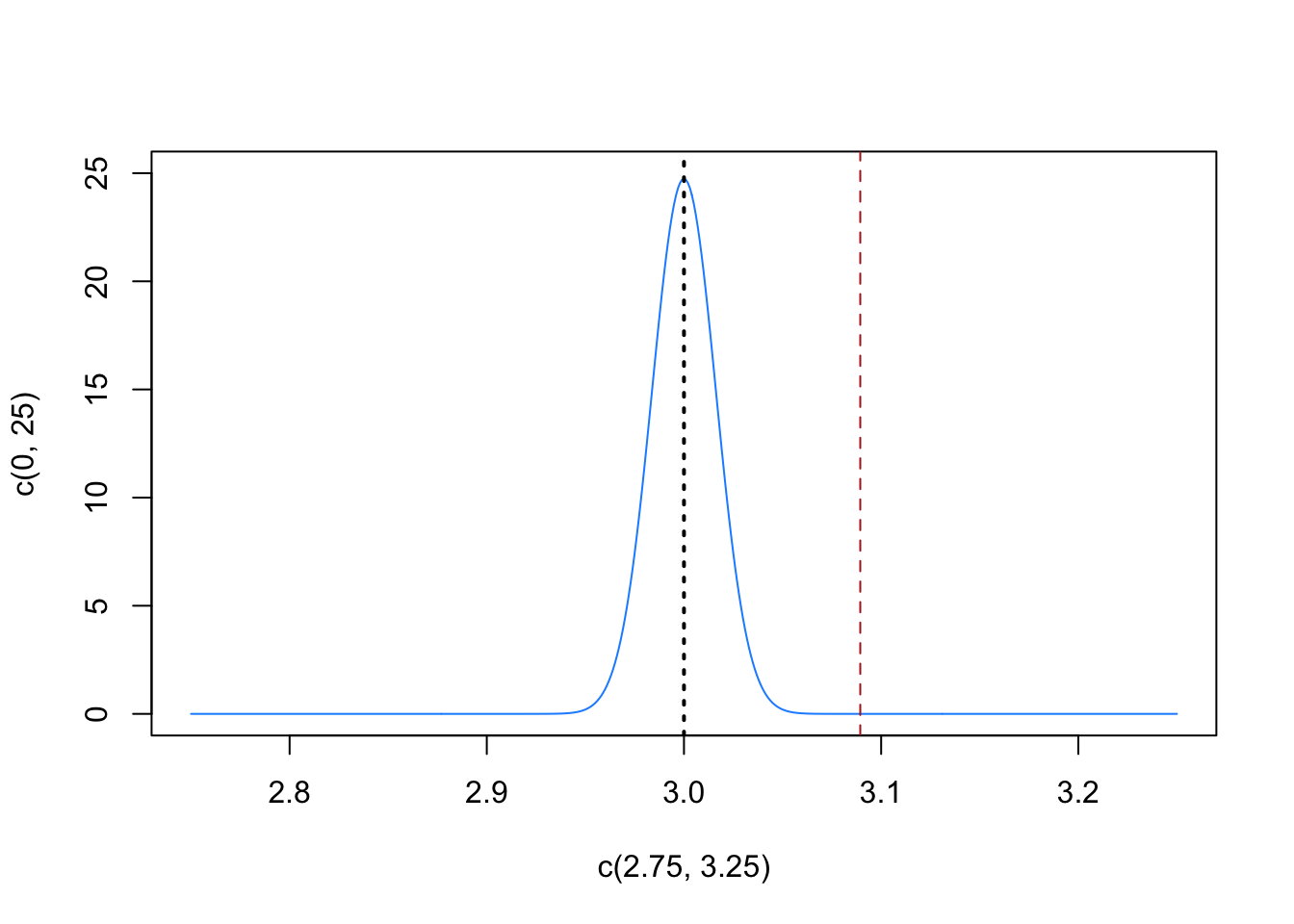
The blue distribution is just like the simulations that we did above of coin flips: it describes the probability of different outcomes due to random sampling if the true ideology of Pennsylvanian’s was 3. In this case, however, we didn’t get it by simulating a large number of times, but instead through mathematics and the standard error. This distribution would allow us to conclude that it would be very unlikely to get a sample mean for ideology of 3.1 if the truth was that Pennsylvanians’ true average ideology was 3.
And critically, the process which we used to get there does not rely on any assumptions about the underlying process (like we did with coin flips) and we can apply the process to any sort of mean that we want. Whenever we get a mean in our data, we can determine the amount of variation that will be caused by random sampling by calculating \(\frac{sd(x)}{\sqrt{n}}\).
The equation for the standard error makes good logical sense. What determines the amount of sampling variation? How variable the variable is \(sd(x)\) and how big of a sample size you have.
We can look at how the standard error for our ideology average would change for different sample sizes, from 10 people all the way up to 10000 people:
se.n <- sd(pa.dat$ideo5,na.rm=T)/sqrt(10:10000)
plot(10:10000, se.n, type="l")
abline(v=4369, lty=2, col="firebrick")
The square root in the denominator of the equation for the standard error means that as you add more people to the sample the standard error declines, but at a declining rate. That is: going from 10 to 100 people matters a lot for reducing how much a mean will vary from sample to sample. Going from 100 to 200 people matters too, but not as much as going from 10 to 100 people. Going from 200-300 matters even less. We can see on the above graph that the gains to efficiency bottom out past around 1000 people.
1.4 Random Sampling (Think of the Soup)
Now all of the above assumed that the samples being taken were random samples of whatever it is that we are looking at. In the context of an election poll, traditional methods have you generate random phone numbers to call so that everyone in the US has an equally likely probability of being included. (Modern polling is slightly more complicated than this, which we can get into at a later date).
Random sampling is really what allows for the magic of statistics, and everything falls apart without it.
One clue to it’s importance comes from the equation for the standard error I presented above: \(\frac{sd(x)}{\sqrt{n}}\). For a mean, the amount of random noise that is to be expected is a function of how random our sample is (the standard deviation) and the sample size. One thing that is not in this equation is the size of the population.
This tells us, in other words, that a random sample of 1000 people has the same ability to tell us something about the population of Canada (33 million people) as it does for the population of the US (330 million) as it does for China (1.4 billion). As long as the sample is a random sample, the standard error for all three estimates will be the same.
How can this be? The best way to think about this is to think about soup. When you are making soup (I know you are all undergrads and don’t cook but you can imagine what it might be like to make soup) and you want to know if it tastes good, do you have to eat a huge bowl? No! You stir it up (randomization) and take just one spoonful to see how it tastes. It wouldn’t matter if you had a 1 quart or 30 quart pot, to see how it tastes you would still just take one spoonful (conditional on it being well mixed, which is the randomization part!)
1.5 The Big Picture
So what do I want you to know about statistics in this “not statistics” course?
Primarily, I want you to keep in mind that the things we are doing in this course – while vital! – are only one leg of the “data science” pyramid. We are going to learn a lot about loading, cleaning, manipulating, and presenting data. This work will be hard and I promise you will learn a lot of great skills. But these skills are fairly limited in isolation.
To this knowledge you will learn more about statistics. For right now, it’s enough to remember that every dataset we look at is one of an infinite number of datasets we could have. That means every thing we estimate is one of an infinite number of estimates we could have. To properly understand the estimates in our dataset we need a measure of how much noise is likely to occur based on these differences from sample-to sample.
We are going to talk about hypothesis testing down the road, which will give you some tools to use this information. But really, I encourage you to take further courses in statistics to properly understand this.