2 Basic R
2.1 Why R?
This course teaches the foundations of doing data science work using the R programming language. You probably decided to take this class because you are interested in data science and have heard that R is a helpful thing to know in order to work in that space.
But why is this the way that we do things? In particular, Excel is right there and does a lot of the same things that R does. And does them in a much easier way. Why are we making this so hard on ourselves?
Here’s a cautionary tale. In 2010 Economists Carmen Reinhardt and Ken Rogoff published a paper in the American Economic Review detailing the relationship between the amount of debt a county had and their growth in GDP. Critically, they found that there was a profoundly negative relationship between these two things, as the figure below shows. This finding was used widely by central economic authorities in the aftermath of the financial crisis to push low-debt austerity measures.
Another team of Economists were skeptical of these findings so they downloaded the same data and re-ran the analyses in the paper. This is what they found:
There is some effect of taking on debt at very low ranges, but once you get to about 40% debt to GDP ratio there really isn’t any effect.
So what happened here? In short, the original authors were using Excel and made a few bone-headed coding errors. One of the errors they made was that they didn’t drag a formula all the way to the bottom of a column. Because of this, a good chunk of the data simply was left out of their analysis.
If you are more into the natural sciences, how about this: 30% of published papers on genetics are wrong because the authors use Excel. The errors here are due to Excel’s over-zealous conversion of numbers into dates and scientific notation. An actual genetic marker is “SEPT7” which, of course, Excel converts to September 7th. Another maker is “2310009E13” which Excel converts to “2.31E+13”.
So is the lesson here: Excel does things wrong and R doesn’t? Not really. As we will see you can absolutely make mistakes in R.
The difference is not in the ability to make mistakes, but the ability to find, identify, and reverse those mistakes after you’ve made them.
We are going to use R in a fundamentally different way than how we use Excel.
If I was working with data into Excel, I would load it in, make a bunch of changes – maybe reformatting some variables, calculating new variables, choosing variables to put into a regression – and then I would save what I have done so I can pick back up on that work the next time I sit down at my computer. But critically, I will have no record of exactly what I did the last time I worked, I just have this new, altered, dataset to work with.
In R (and many other programming languages) instead of constantly saving our data and output, we instead save a script that tells us all the steps we need to take to go from our raw data inputs to our polished final outputs. Because each step of the process is recorded, we can review those steps to find potential mistakes. More importantly, we can un-do those mistakes by just changing a couple of lines. We also never have to worry about making un-reversible changes because we accidentally saved the wrong version of the dataset.
All of science needs to assume human fallibility in it’s process. We all make mistakes. It’s contingent on us as data scientists to put systems in place to minimize the impact of those mistakes.
For what it’s worth R&R deflected criticism, never admitted to anything, and kept making the same arguments even though their data didn’t support them. At least one genetics researcher interviewed about problems in that field said that she doesn’t have time to learn R, and that the quirks of Excel is “One of those things that I just accept.”
Both truly unhinged responses.
2.1.1 The Three Rs of Good Coding
Broadening out, I think about there being “Three Rs” to good data science coding that I want you to internalize through this course. Good coding is:
- Replicable
Can someone (or more likely, you in the future) understand what you’ve done and do it themselves? The way that we meet this goal is to write well formatted scripts that give a full record of what we did from raw data to output. Additionally, we make comments in our code to make clear the decisions we are making so that people in the future are clear about what we did.
- Reversible
Everything that happens between downloading a data set from the internet to producing a figure needs to be documented. And we should always start from that raw data input (that never gets changed). We never do any pre-processing in Excel. “But it would be so easy to go in an delete that header that we aren’t using”. No! The potential of making a mistake you can’t find later is too high. These steps together make our code reversible. We can always go back to the start and re-run our script to the point we made a mistake and to undo it.
- Retrievable
To do any work as a data scientist you must understand the file system on your computer. You must know where you have stored things and be able to find those scripts and data when you need to. You should understand folders and sub-folders, and how to organize them in a way that will make sense to other people and to future you.
It has become a bit of an obsession that the current generation of students don’t understand where files are stored on their computers. I have been around universities for a while and there is always some version of “kids these days” so I generally discount any grumbling like this. That being said, the ubiquity and genuinely incredible ability of Spotlight search on Mac has pushed people of your generation to discount the importance of organizing files. It pushes you towards thinking about your computer as a “laundry basket” where you store all your files (maybe on the desktop, maybe in downloads) and then use spotlight to find those files when you need them.
The proper system for serious data work is to use the “nested file drawer” system, where things are organized hierarchically.
On Canvas there is an “Example Problem Set” folder that highlights how this should work.
On my computer this folder is located at
'/Users/marctrussler/PORES Dropbox/PORES/PSCI1800/Problem Sets/Example Problem Set Folder'
On my Macbook there is a folder for my (marctrussler). In that folder I have saved my dropbox folder. Within that Dropbox Folder are many things, including a shared folder for PORES. In that folder are course notes for many courses, including this one. In that folder I have a specific folder for Problem Sets. In that folder I have an example problem set folder. In that folder I have specific places to store code and data and figures. I would tell R that this is the folder I am working out of and it would know where to look for data, or to save figures. In the future if I want to reference this problem set (and I actually look through my old problem sets from grad school all the time) I know exactly where to look for it.
Part of my job as a professor is tough love, so here it is: if you want to work in this field you have to understand the file structure on your computer and use it. You will not be taken seriously otherwise. I don’t care that it’s easy to find files with Spotlight. In the final project of this course you will send me a zipped folder that contains your final work, along with all the code and data that produces that final work. If that’s not organized in a proper format (and we will talk about what that format is!) you will fail the project.
Additionally, you will notice that where I am working is out of my dropbox drive. All of the major cloud backups (icloud, dropbox, google drive, box) work by simultaneously storing files both on your physical hard drive and in the cloud. Every time you save a file that is saved in one of these locations it is backed up the cloud automatically. Because everything I do is backed up the cloud, I could walk down to the Schuykill, throw my laptop in, and tomorrow I would be back up and running on all my projects as if nothing had happened. All data science jobs will expect you to do the same. While it’s not a requirement: I’m telling you right now that this is very easy to do. If you come to me in 2 months and tell me that you spilled coffee on your laptop and next an extension, I will refer you back to this paragraph.
2.1.2 How do you get good at R?
It is helpful to take the approach with this stuff that you are genuinely learning a new language. That makes this class very different from other classes at Penn where you are building on previously existing knowledge and skills. You are goign to be hit with a steep learning curve here similar to if you were enrolled in Swahili.
By nature of being Penn students you are used to being good at things. Learning a new programming language necessitates being bad at something, at least for a little bit. I have found, sometimes, that students in my class find this transition a bit tough. Being bad at something requires a different sort of work ethic that you may not have had to practice in a while. Those of you who are most likely to succeed are those that “embrace the struggle” and get good at being bad.
What does that look like?
First, understand that you just aren’t going to get to the right answer right away. You are going to have to sit and not know what to do, and you should feel confident that you will get to the right answer and it’s ok that you don’t have it right away.
Relatedly: know when and when not to ask for help. Try not to bail out of problems right away. Really give it a good go by yourself before reaching out for help. Relatedly: while collaboration is allowed on problem sets, it is a huge benefit to work through the entire problem set on your own first before you shift to collaboration.
Finally: know where to get information to help you solve the problems. You will have this e-textbook, but I would encourage you to take notes on important concepts in addition to what is here. Keep the R files I give you organized and know what is in each one. If, on a future problem set, you know that you have to work with date information, you need to be able to quickly locate examples of where I did that. You don’t want to be fumbling around not able to find an example you know exists for 30 minutes.
When I think about how and when I “got good” at R, I think about sitting at my desk in grad school at like 9 or 10 o’clock the night before I had a problem set due. There was no one around to ask questions to, so I just had to sit there and figure it out. While I don’t want you to have to struggle (and I would encourage better sleep habits than I had in grad school), don’t discount the real transformative power of sitting with a problem until you figure it out.
2.2 Basic R
2.2.1 The R Studio Environment
#This is a command that clears everything out of the "environment" giving us a blank slate:
rm(list=ls())Welcome to R!
Right now you should have R studio open.
You are looking at 4 different “panes” or mini-windows.
The actual program “R” is running in the bottom left window, called the “console”. If we just opened the program R on our computer this is exactly what we see. Technically, we could just type the stuff we want to do down there. However, that would mean that we would have no record of what it is that we have done.
The top left is the most important window called the “script” window. This is where we are going to do most of our work and write most of our code. We will talk about why we want all of our code written here, but in short it is so we have a full, saved, record of everything we have done. We will see that we can select lines of code (or many lines of code) to be sent to the console to be run.
The top right window is the “environment” which will show pieces of information (what we call objects) that R currently has loaded into memory. Eventually this will include full datasets.
The bottom right window has a few functions, the most important of which is to display plots that we create.
All of this is highly customizable. Open Tools>Global Options to see different ways you can organize your R studio window.
2.2.2 R is just a fancy version of Excel
While R is a huge improvement over Excel in terms of replicability, reliability, and retrievability, at it’s most basic level we can think about it as a fancy version of that program.
R is a program that applies math to rows and columns of data. It is doing so in a slightly more convoluted way, but hopefully the negative examples above help motivate why it is that we are doing it this way.
At the most basic level we can use R as a basic calculator.
If we, for example, type 4+3 into the console it will spit out 7. We can also do something like sqrt(2) and it will give us the answer.
But we can also type those same things into the script window and execute them from there. If we highlight the code that we want to execute and press the Run button in the top right of the script window it will “type” that command into the console for you.
4+3
#> [1] 7
sqrt(4)
#> [1] 2
sqrt(4) + 2
#> [1] 4Instead of hitting the Run button we can alternatively use ctrl+enter on a Windows computer and cmd+enter on a Mac computer. Additionally, if we use any of those commands when we are not highlighting anything, R will run the full line of code.
One helpful trick is that if we put out cursor in the console and hit the up and down arrows on our keyboard, R will cycle through the most recent commands that have been executed.
A special character in an R script is a #. This is what we use to make comments in our R script. Anything placed after a # will not be evaluated by R. In other words it will be ignored. We can use that to make comments in our code.
#This Line is commented outThere are a couple of small syntax things that are helpful to know in R.
If you forget to close a parentheses, R will wait for you to finish what you are doing:
If you un-comment and try to run the first line of what is below, the console will show a + sign. This is R saying “I’m expecting more information!” To deal with this, you can either give it the closing parentheses (un-comment the second line and run that), or you can put your cursor in the console and press the Esc key. This will reset the console.
#sqrt(4
#)R will ignore spaces. For example these two commands are treated the same:
Some other basic math functions to know:
#Division
5/3
#> [1] 1.666667
#Multiplication
5*3
#> [1] 15
#Exponents
5^3
#> [1] 125
#Using parentheses:
5*(3+3)
#> [1] 30
#Incorrect (Need the multiplication sign)
#5(3*3)But this wouldn’t be very interesting if R was just some fancy calculator. What is interesting about R is when we can store and later manipulate pieces of information.
In R we create “objects”. We can think of these as shortcuts to stored information. What is contained in an object is nearly endless. It can be single numbers, a combination of numbers, whole datasets, results from regression models….
To start with we can store the output of a simple mathematical statement as an object called result
result <- 5+3After running this, we can see that there is now an object stored in our environment called result, and that object represents the number 8.
If we now type and run result R will return the number 8.
result
#> [1] 8And we can now treat the word result as if it is the number 8.
result + 2
#> [1] 10Note that there is nothing special about the word result here. We could have called this anything. For example:
batman <- 5+3
batman
#> [1] 8Nothing in R will stop you from overwriting an object we have already stored. For example if we now define batman as being equal to something else, no warning will pop up telling us not to do that.
batman <- "Bruce Wayne"
batman
#> [1] "Bruce Wayne"But that’s not a problem in R! We aren’t making any sort of permanent, saved, changes. If we simply go back and re-run our script to the place where we made a mistake we will undo the mistake. We don’t need an undo button because we have a map of exactly how we got to the point before we made the mistake!
It’s important to note that nearly everything in R is case sensitive so if we un-comment and try to run:
#BatmanNothing will happen! That’s treated as a separate name from batman.
Notice that when we look in the environment “Bruce Wayne” is in quotation marks. Quotation marks indicate that a piece of information is in the “character” class, which just means it is being treated as text. There will be special things that we can do when a piece of information is text, but one thing we cannot do is math.
So if we tried to do:
#(Uncomment the below)
#batman/8We get an error that we are trying to do math on something that isn’t a number.
This is even true if we define capital-R Result to be 8 in quotation marks:
Result <- "8"
#Uncomment the below line
#Result/8Even though we can divide the number 8 by 8 to get 1, in this case we have explicitly told R to treat this like text instead of as a number, and it will do so. This particular error non-numeric argument to binary operator is a good one to remember because it will come up when we are loading in data from the internet. For example if we load in a datafile and a column is population but somewhere in the 2933rd row it says “population unknown”, R is going to treat the whole column as if it’s text. If we try to perform math on that column we would get that error.
2.2.3 Functions
We have learned that we can save pieces of information as objects. The next step in R are “functions” which are ways that we apply some sort of process to an object.
If we want to take the square root of 8 we could do:
8^.5
#> [1] 2.828427But that’s cumbersome. Helpfully the makers of R have given us a shortcut function sqrt() that we can apply to anything to get the square root.
sqrt(8)
#> [1] 2.828427We can apply these functions to objects, if it makes sense to do so:
#Yes
sqrt(result)
#> [1] 2.828427
#No
#sqrt(Result)There are functions for words too, don’t worry!
nchar(batman)
#> [1] 11All functions will work similarly where we will write the name of function, and whatever we are inputting into the function will be within parentheses.
Another helpful function that builds on what we’ve already done is class(), which will tell us what type of object something is:
class(Result)
#> [1] "character"
class(result)
#> [1] "numeric"
class(sqrt)
#> [1] "function"
#(These are not all the classes)2.2.4 Vectors
So far this doesn’t look much like excel where we are often working with whole rows and columns of data.
To start getting in that direction, we can create a “vector” which is a whole series of numbers stored together.
To start, we can create a vector world.pop that is the world population (in millions) every decade from 1950 to 2010.
world.pop <- c(2525,3026,3691,4449,5320,6127,6916)The function we used to combine these numbers together is c() which stands for “concatenate”. This function will combine things together into a row of numbers.
We can see that world.pop is now stored in the environment, and looks somewhat different to the objects that just represent one number or word.
If we run world.pop it will return all 7 of the numbers:
world.pop
#> [1] 2525 3026 3691 4449 5320 6127 6916We can also use c() to combine multiple objects together into a longer vector:
One of the most important functionalities in R is the use of square brackets [] to pull out specific items from a vector (And eventually, a dataset). This square bracket functionality is absolutely fundamental to using R.
We have world.pop which is a vector with 7 entries. If this was excel we could visually see those 7 entries. We could click on one of the items and change it, if we wanted to. In R we don’t have that visual interface with the data we have stored. In replacement, we can use square brackets to interact with stored pieces of information.
In the environment we see world.pop num [1:7] that last piece of information is telling us that world.pop has 7 entries in it. We can use square brackets to access pieces of information. If we put the square brackets after the vector and put in a number, it will give us that entry in world.pop:
#The second item in world.pop
world.pop[2]
#> [1] 3026
#The third entry in world.pop
world.pop[3]
#> [1] 3691What if we wanted the 2nd and 5th entries to world.pop?
Here we have to start combining what we’ve learned so far. How do we combine together the numbers 2 and 5 in R? Concatenate!
world.pop[c(2,5)]
#> [1] 3026 5320What if we want the 2,3,4 entries to world.pop? Well we can absolutely do:
world.pop[c(2,3,4)]
#> [1] 3026 3691 4449But what if world.pop was thousands of lines long and we wanted the first 1000? We aren’t going to do c(1,2,3,4,5,6,7,....). Instead, we can create a vector of consecutive integers using a colon:
2:4
#> [1] 2 3 4
1:25
#> [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
#> [19] 19 20 21 22 23 24 25Applying that to our vector:
world.pop[2:4]
#> [1] 3026 3691 4449If we want to do the opposite, returning the vector without a certain entry, we can use a minus sign:
world.pop
#> [1] 2525 3026 3691 4449 5320 6127 6916
world.pop[-3]
#> [1] 2525 3026 4449 5320 6127 6916Just like in Excel, we can apply a math equation to a vector and it will apply it individually to each item in the vector:
world.pop*1000000
#> [1] 2.525e+09 3.026e+09 3.691e+09 4.449e+09 5.320e+09
#> [6] 6.127e+09 6.916e+09What if we wanted to create a new object, that was the world population in each year as a proportion of the world population in 1950?
This is a straight-forward application of what we have done already:
world.pop/world.pop[1]
#> [1] 1.000000 1.198416 1.461782 1.761980 2.106931 2.426535
#> [7] 2.739010
pop.rate <- world.pop/world.pop[1]
pop.rate
#> [1] 1.000000 1.198416 1.461782 1.761980 2.106931 2.426535
#> [7] 2.739010OK we have world.pop and pop.rate but these two things are sort of just floating in space and are unconnected. It would be nice if we could treat them like a little table and visually see which numbers paired together.
Let’s create a little table, and while we are at it, let’s create a vector of years so we know what each entry refers to.
year <- c(1950,1960,1970,1980,1990,2000,2010)Can we use c() to put these three things together?
c(year, world.pop, pop.rate)
#> [1] 1950.000000 1960.000000 1970.000000 1980.000000
#> [5] 1990.000000 2000.000000 2010.000000 2525.000000
#> [9] 3026.000000 3691.000000 4449.000000 5320.000000
#> [13] 6127.000000 6916.000000 1.000000 1.198416
#> [17] 1.461782 1.761980 2.106931 2.426535
#> [21] 2.739010We can try! but this is just going to stack them all up into one long vector. That’s not what we want!
Instead we are going to use the cbind() function, which stands for “column bind”. (There is also a rbind() function for rows). This accomplishes something very different than c()! It takes vectors of the same length and combines them together into a small table.
cbind(year,world.pop,pop.rate)
#> year world.pop pop.rate
#> [1,] 1950 2525 1.000000
#> [2,] 1960 3026 1.198416
#> [3,] 1970 3691 1.461782
#> [4,] 1980 4449 1.761980
#> [5,] 1990 5320 2.106931
#> [6,] 2000 6127 2.426535
#> [7,] 2010 6916 2.739010
#We can, of course, save this:
population.table <- cbind(year,world.pop,pop.rate)
population.table
#> year world.pop pop.rate
#> [1,] 1950 2525 1.000000
#> [2,] 1960 3026 1.198416
#> [3,] 1970 3691 1.461782
#> [4,] 1980 4449 1.761980
#> [5,] 1990 5320 2.106931
#> [6,] 2000 6127 2.426535
#> [7,] 2010 6916 2.739010What if we want to add another variable to our table. Let’s say we also want to record what the c02 emissions (in billions of tonnes) were in each decade. We can first make that into a vector:
emissions <- c(6,9.33,14.83,19.37,22.7,25.12,33.13)We want to cbind this to our table. We could re-run our original cbind command with emissions now added in the list:
cbind(year,world.pop,pop.rate, emissions)
#> year world.pop pop.rate emissions
#> [1,] 1950 2525 1.000000 6.00
#> [2,] 1960 3026 1.198416 9.33
#> [3,] 1970 3691 1.461782 14.83
#> [4,] 1980 4449 1.761980 19.37
#> [5,] 1990 5320 2.106931 22.70
#> [6,] 2000 6127 2.426535 25.12
#> [7,] 2010 6916 2.739010 33.13But we could also simply cbind on the new column to our already existing table
population.table <- cbind(population.table, emissions)Similar to when we have a single vector, we want to be able to access the information we have stored in population.table. We can see in the environment that population.table is in its own section, “Data”. Further, it now says population.table num [1:7,1:3]. This is giving us a clue on how we are going to access this information. If we look at pop.rate it tells us that there are 7 values we can access using square brackets. Now that we have put things into a table we see that there are 7 rows that we can access and 3 columns.
The square bracket functionality extends to a table where we can use [row,colum] to access information.
So if we want to see the 1st entry in the 3rd row:
population.table[3,1]
#> year
#> 1970Or the 3rd entry in the 1st row
population.table[1,3]
#> pop.rate
#> 1More importantly, we can pull out entire rows and columns.
If we wanted the whole 1st row we could do:
population.table[1,1:3]
#> year world.pop pop.rate
#> 1950 2525 1But much easier, if we leave one of the row or column spots blank, it tells R: give me all of the rows (or columns):
population.table[1, ]
#> year world.pop pop.rate emissions
#> 1950 2525 1 6So to get the whole second column:
population.table[ ,2]
#> [1] 2525 3026 3691 4449 5320 6127 6916Now that we can do that, we can run functions on individual columns. Here are some common things we might want to know:
mean(population.table[,2])
#> [1] 4579.143
min(population.table[,2])
#> [1] 2525
max(population.table[,2])
#> [1] 6916
range(population.table[,2])
#> [1] 2525 6916
sum(population.table[,2])
#> [1] 32054These functions are pretty key to doing data science work. One important thing to note though is that there is one particular circumstance that breaks them.
Let’s say that we didn’t know the world population in 1980. How would we represent that information.
It’s tempting to just leave it out and define world.pop as:
world.pop2 <- c(2525,3026,3691,4449,6127,6916)But then how would we combine that with the other pieces of information that have 7 entries? R isn’t going to know to skip a spot and leave exactly that position blank…
What about this?
world.pop2 <- c(2525,3026,3691,4449,0,6127,6916)That solves the problem of needing to have 7 entries, but 0 is a real number! It’s going to massively screw up taking the mean, for example, if we put 0 in.
Instead, R has a special class of object for missing data: NA. This is not the same as zero. This holds a place in a vector, but is treated as missing data
We can set the world.pop and pop.rate numbers for 1980 to be NA like this:
population.table[4,2:3]
#> world.pop pop.rate
#> 4449.00000 1.76198
population.table[4,2:3] <- NA
population.table
#> year world.pop pop.rate emissions
#> [1,] 1950 2525 1.000000 6.00
#> [2,] 1960 3026 1.198416 9.33
#> [3,] 1970 3691 1.461782 14.83
#> [4,] 1980 NA NA 19.37
#> [5,] 1990 5320 2.106931 22.70
#> [6,] 2000 6127 2.426535 25.12
#> [7,] 2010 6916 2.739010 33.13Now when we look at the table clearly those two things are missing.
What happens now if we try to take the mean of the 2nd column?
mean(population.table[,2])
#> [1] NAWe get an NA back. This is a quirk of R that is actually helpful down the road (in short we don’t want to get a misleading mean if we having missing data) but right now just means we have to explicitly tell R to calculate the mean by ignoring the missing piece of data.
To do so we are going to add an “option” to the mean command. To add an option in a function we will use a comma and then put in the thing we want to change.
mean(population.table[,2],na.rm=TRUE)
#> [1] 4600.833So here, the option we changed is changing na.rm=FALSE, which is the default, to na.rm=TRUE. There will be many such options for nearly all functions. Indeed, if we do the following we will see all the options for the mean() function
#?meanWe would have to do the same na.rm=TRUE option for sum and median and min and max…
Miraculously we’ve rediscovered the missing data, so let’s add that back in:
population.table[4,2:3] <- c(4449,1.76198)
population.table
#> year world.pop pop.rate emissions
#> [1,] 1950 2525 1.000000 6.00
#> [2,] 1960 3026 1.198416 9.33
#> [3,] 1970 3691 1.461782 14.83
#> [4,] 1980 4449 1.761980 19.37
#> [5,] 1990 5320 2.106931 22.70
#> [6,] 2000 6127 2.426535 25.12
#> [7,] 2010 6916 2.739010 33.132.2.5 Loading Data: two ways
Writing our own columns of data and binding them together is not a very satisfying experience. In this class (and in your life) the primary use of R is not as a data-entry tool but rather a tool for manipulating already existing data. To get to that stage we need to learn how to load data into R.
Before we get there we need to make one customization to R on our computers. R has a large amount of “base” functionality. We have seen functions like cbind() or mean(). These are things that come stock with R. Think of these like the programs that are already installed on a new computer.
One nice thing about R is that it is “open source” meaning that anyone can develop new functions for R that make life easier. Think of this like downloading and installing a new program on a laptop. These new functions we can download are called “packages”.
A helpful package for loading data is called rio. Luckily, we don’t need to go to a website or click through a bunch of menus to download a package. R will actually do it all for you (contingent on being connected to the internet).
We can un-comment and run the following line:
#install.packages("rio")R will think for a little while, but eventually you will get a big DONE.
We have done the equivalent of downloading and installing a new program, but like doing this on your laptop, if we want to actually use this program we need to open it. We do so with the following command:
#Note that rio is *not* in quotation marks
library(rio)
#If it prompts you to you should also un-comment and run:
#install_formats()If we want to check that we have done the right thing, we can click the “packages” tab in the lower right pane of Rmarkdown, scroll to “rio” and see that there is a check mark by it.
Now we have the tools we need to load in some data.
To make things easier for you in this class I have uploaded nearly all of the data we are going to use to the internet. This means that you can just load the data in using the code I provide without downloading anything.
For example, we can load in 1000 survey responses about whether someone went to college (1) or not (0) using:
college <- import("https://github.com/marctrussler/IDS-Data/raw/main/college.Rds")
#> Warning: The `trust` argument of `import()` should be explicit for
#> serialization formats as of rio 1.0.3.
#> ℹ Missing `trust` will be set to FALSE by default for RDS
#> in 2.0.0.
#> ℹ The deprecated feature was likely used in the rio
#> package.
#> Please report the issue at
#> <https://github.com/gesistsa/rio/issues>.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where
#> this warning was generated.The import command is what we are using the rio package for. This command helpfully automatically identifies the file format of what we are loading in. Here we are loading in a “.rds” file, which is Rs native method of storing data. There should now be a new vector college in your environment. Let’s load in 3 other vectors from this same survey of 1000 people:
education <- import("https://github.com/marctrussler/IDS-Data/raw/main/education.Rds")
income <- import("https://github.com/marctrussler/IDS-Data/raw/main/income.Rds")
race <- import("https://github.com/marctrussler/IDS-Data/raw/main/race.Rds")Great!
Now I said that there are two ways of loading data to your computer. The other (more complicated) way is to download the data to your computer and load it from your hard drive. While all of the in-class data we use will be loaded via url, you still need to know how to load data on your computers for the final project (and to, you know, use R in your regular life).
I’ve added on canvas the file PACounties.Rds. Download that file, and place it in a properly named folder (see above for what I mean by a properly named folder).
We are going to tell R where this file is so that it can load it.
Now I downloaded the file into the folder on my computer for this class in a sub-folder called “Data”. I’m going to use the file explorer on my computer to navigate to that file on my computer.
Because I’m using a windows computer I’m going to hold down the shift key and then right click the file. When I do this the option “Copy as path” will appear in the menu. I’m going to click that button. We can now paste that filepath into the same import command that we used to load data from the github url. One last complication on a Windows computer is that the “copy as path” trick gives a filepath with the slashes going in the wrong direction. You just have to change the \ to /, which you can do manually or via find-and-replace (ctrl-f).
If you are using an Apple computer (and most of you are) you are also going to navigate to the downloaded file using finder. Right click (control + click, or two finger click on trackpad) on the file and a context menu with options will popup. Hold the option key then the options will change and you would be able to see the option: Copy "folder_name" as Pathname. Click on it, the full path of the file/folder would be copied to the clipboard. You can now paste the full path into the import command. You do not have to change the direction of the slashes.
#You will have to paste your own filepath into the import command
#pa.counties <- import("C:/Users/trussler-adm/PORES Dropbox/PORES/PSCI1800/Data/PACounties.Rds")
#In case you can't get that to work (you really need to figure out how to get it to work)
pa.counties <- import("https://github.com/marctrussler/IDS-Data/raw/main/PACounties.Rds")Why all the hassle to load in data this way???? Why can’t we just go File>Open File and load the data in that way?
One of the best parts of R (eventually) is that it lets you keep open and simultaneously work on multiple datasets at once. When i’m doing work for NBC I may be loading in data from a couple different election cycles, plus data on the demographics of counties, and maybe some polling data. Given the way that we work with R (a script that takes us from raw inputs to polished outputs) it would be a massive pain in the ass if every time I opened R I had to manually go to the File menu and load the 5 or 6 sources of raw data that I need to do the work for that. Instead, I just load the files using code when they are needed and I never have to think about where they are coming from again!
2.2.6 Closing and Opening RStudio
When you are finished your work for the day what should you do? What do we need to save to make sure that we don’t lose anything?
All we need to do is make sure our script is saved. Because we have a record of everything that we did, we can just open R and do that again. (A future exception to this to come below).
When you close Rstudio it’s going to ask you:
Save workspace image to ~/Documents/GitHub/IDS/.RData?
The answer to this question is no, you don’t want to save your workspace image. Indeed, I just turn this option off. (Tools>Global Options>Save Workspace to Rdata on Exit>Never).
If we select this option, everything in your environment will be saved and re-loaded automatically when you re-open R. This seems nice, but has some downsides.
First: I work on a lot of different projects, and I want to make sure I have the right data loaded in for the right project. If i’m working on two different projects that have a dataset called elect, I don’t want to be confused about which one I have open!
Second: Eventually you will start working with larger and larger datasets. Some will have hundreds of thousands of rows of data. If you look at the environment tab you will see a grey circle with some green filled in and then a measurement of data size (this is next to the broom). This is how much of your RAM (or working memory) Rstudio is currently using. Each new dataset that you load in has to be loaded into your RAM, which has a finite amount of space. If you have too much stuff loaded (or just keep everything loaded all the time), this will fill up and massively slow down your computer.
Let me load in a really big dataset:
big.data <- rio::import("https://github.com/marctrussler/IIS-Data/raw/refs/heads/main/FullSamples.rds")We see that my RAM usage has gone up significantly. I don’t want to carry around this data and have it open every time I use R. So when I close and re-open R I’m not going to save my workspace. I’m going to rely on the fact that I have a script that will load and create the right things in the right order to get me back to where I was when I left off.
For right now I’m going to remove that big file manually:
rm(big.data)The exception to “don’t save anything and just use the script to rebuild” will come when you are doing larger projects with a lot of cleaning in them. For these projects, I may have one file that will do a lot of data cleaning, and then I will save a cleaned version of the data (or multiple data sets), that I will then load at the start of an analysis file. I still have a full record of everything I did, I just don’t have to do those steps everytime. This won’t be a practical concern for the types of analysis we are going to do in this class.
2.2.7 Variable types and graphing
We saw on Monday some of the basic ways to assess the information in an individual variable, But here are some more you might want to know. The second columns of population.table is the population, in millions, at the start of each of these decades.
We’ve seen the mean:
mean(population.table[,2])
#> [1] 4579.143But we can also calculate the median value:
median(population.table[,2])
#> [1] 4449Or the standard deviation:
sd(population.table[,2])
#> [1] 1624.968How I like to think about the standard deviation: it’s how much each data point is different from the mean, on average.
We can also get a whole bunch of info at the same time using summary()
summary(population.table[,2])
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 2525 3358 4449 4579 5724 6916Summary gives us the min, max, mean, and median, as well as the 1st and 3rd quartiles of the data. What are these latter two pieces of information? You probably already know that the median is the “middle” value. The value of the data where 50% of the data is lower and 50% of the data is higher. The 1st quartile is similar: it is the value where 25% of the data is lower and 75% of the data is higher. The 3rd quartile is the value where 75% of the data is lower and 25% of the data is higher.
Beyond these simple statistics we are also going to want to visualize some information.
A critical skill we will work on all semester is fitting the right visualization to the data that you have.
We have a bunch of data loaded in so we can think about how to visualize it.
The first type of variable we can think about is a variable that has exactly two values: 1 or 0. I usually call this an “indicator” variable, but you might also hear it referred as a “binary” or “dummy” variable. I like “indicator” because it literally “indicates” the presence of a certain feature. For example, For example, we have a variable college in the data we loaded in that indicates whether each individual has a college degree or not.
Here are the first 6 entries in that vector:
head(college)
#> [1] 1 0 1 0 0 0We can take the mean of this variable, which helpfully tells us the percent of these people with a college degree:
mean(college)
#> [1] 0.499It’s worth emphasizing this mathematical fact: the average of an indicator variable gives the proportion of 1s.
The way that we get the mean is that we add up all the values and divide by the total.
\[ \bar{x} = \frac{\sum_{i=1}^{n} x_i}{n} \]
If a variable that was \({1,0,1,1}\) then that would be \[ \bar{x} = \frac{1+0+1+1}{4}\\ = \frac{3}{4} \]
Just very mechanically because of how the 1s and 0s get added up we get the total number of 1s in the numerator. Because we divide this by the total number of observations in the denominator, it returns the probability of the variable being a 1.
We can find the median value of this variable, but it’s not a particularly interesting thing to find when the variable only takes on 2 values.
median(college)
#> [1] 0When a variable has a distinct and countable number of categories we can use the table() function to determine the relative frequency of those categories. Here we have two categories so we can figure out how many 1s and how many 0s there are:
table(college)
#> college
#> 0 1
#> 501 499This does not make sense for a variable if it has an infinite number of categories. Like if we put income into table we get gibberish:
head(table(income))
#> income
#> 30030.4863229394 30114.9520743638 30324.3792336434
#> 1 1 1
#> 30827.2228762507 30936.6982150823 31300.6469327956
#> 1 1 1How can we visualize an indicator variable. Honestly: most of the time I wouldn’t. I would just say what the mean is because that captures all of the information. But if you wanted to, you could use a histogram:
hist(college)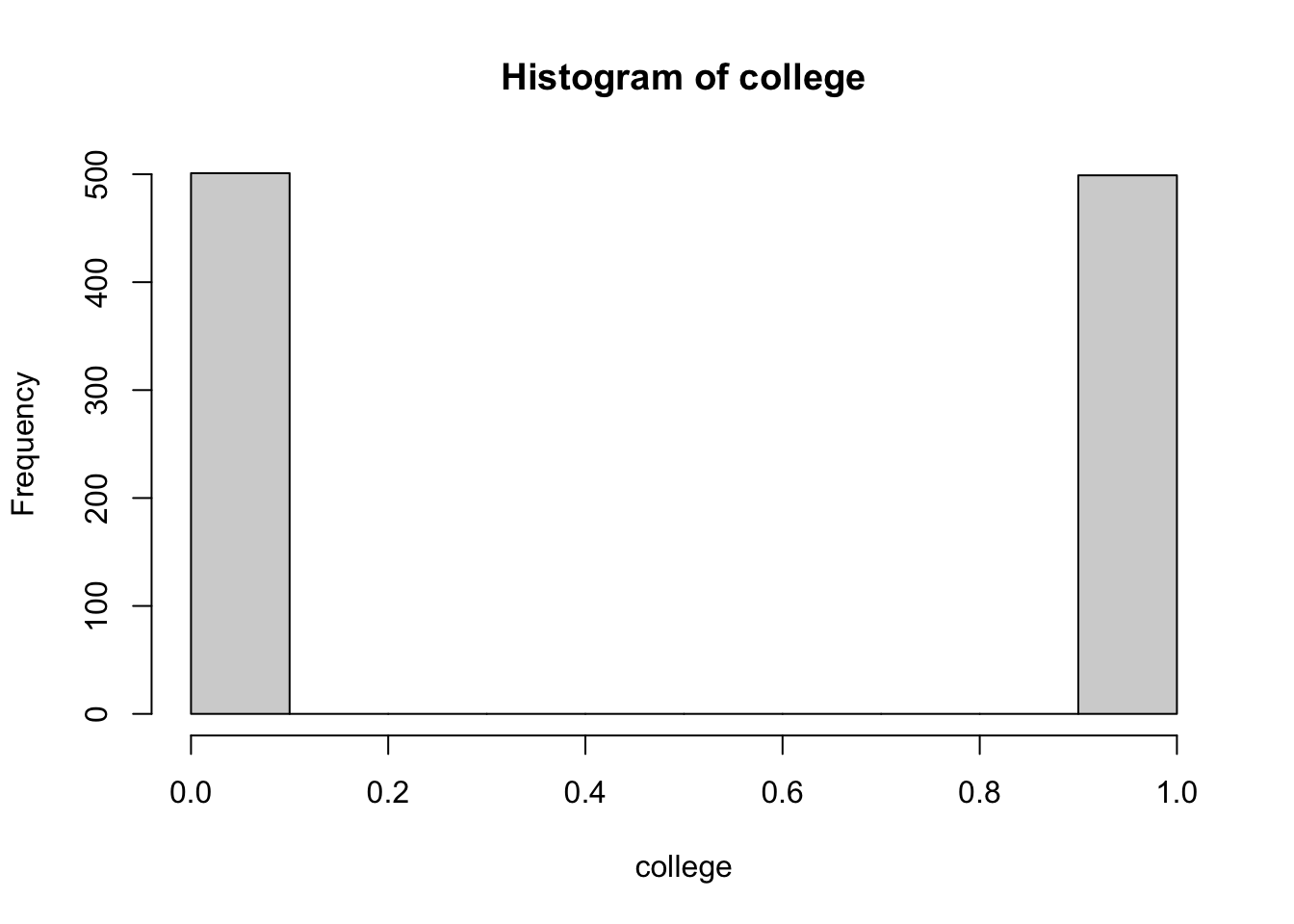
The second type of variable is a categorical variable. This is a non-numeric variable that has a finite number of options that indicate the presence of being in a certain variable.
For example, race is a categorical variable:
head(race)
#> [1] "other" "other" "black" "asian" "black" "white"This is just text data, so taking the mean won’t do anything:
mean(race)
#> Warning in mean.default(race): argument is not numeric or
#> logical: returning NA
#> [1] NAIt’s not even clear what a “mean” of this variable would represent. This is just text.
But we can figure out the relative frequency:
table(race)
#> race
#> asian black other white
#> 239 253 268 240And we can visualize that information by putting it into a barplot:
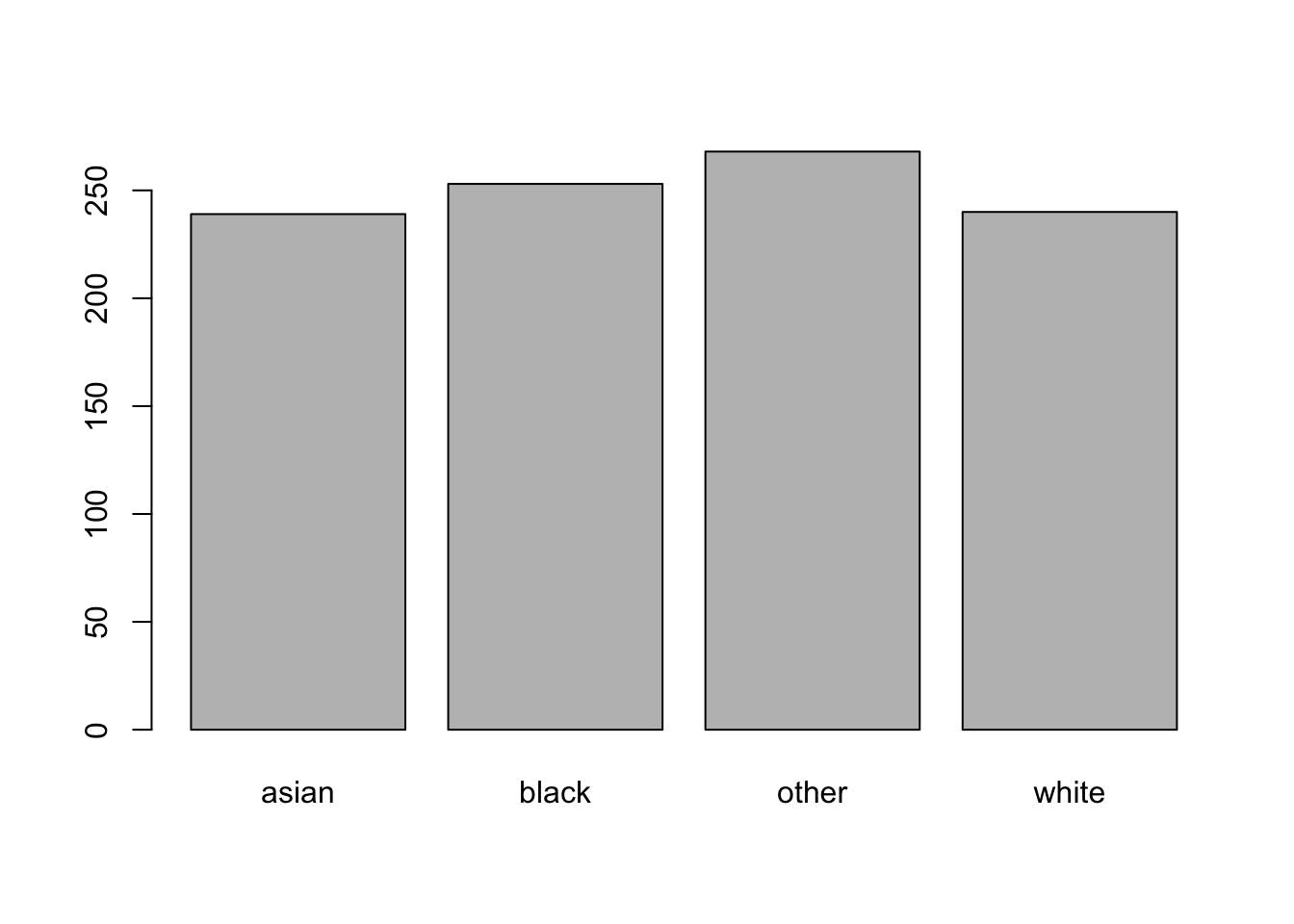
If we want the proportion in each category we could divide by the total:
table(race)/1000
#> race
#> asian black other white
#> 0.239 0.253 0.268 0.240But there is also just a command prop.table() that will do this for us. What we need to do is to wrap our existing table in this secondary command and it will give us the proportions:
prop.table(table(race))
#> race
#> asian black other white
#> 0.239 0.253 0.268 0.240This is the preferable option because prop.table() will take into account missing data. All 1000 people might not have a non-missing value for race, so the correct denominator might be 998 or 900 or 750….. prop.table() will figure this out for us and return the right proportions.
The third variable type is ordinal, which is really a subset of categorical This is a variable that has a finite number of options that indicate the presence of being in a certain category, and those categories are ordered. A great example of this is education:
head(education)
#> [1] "College" "High School" "College" "High School"
#> [5] "High School" "High School"As with an un-ordered variable, we can use a table to find the relative frequency of these categories:
table(education)
#> education
#> Advanced Degree College
#> 256 256
#> High School Less than High School
#> 240 248And use a barplot to visualize the relative frequency:
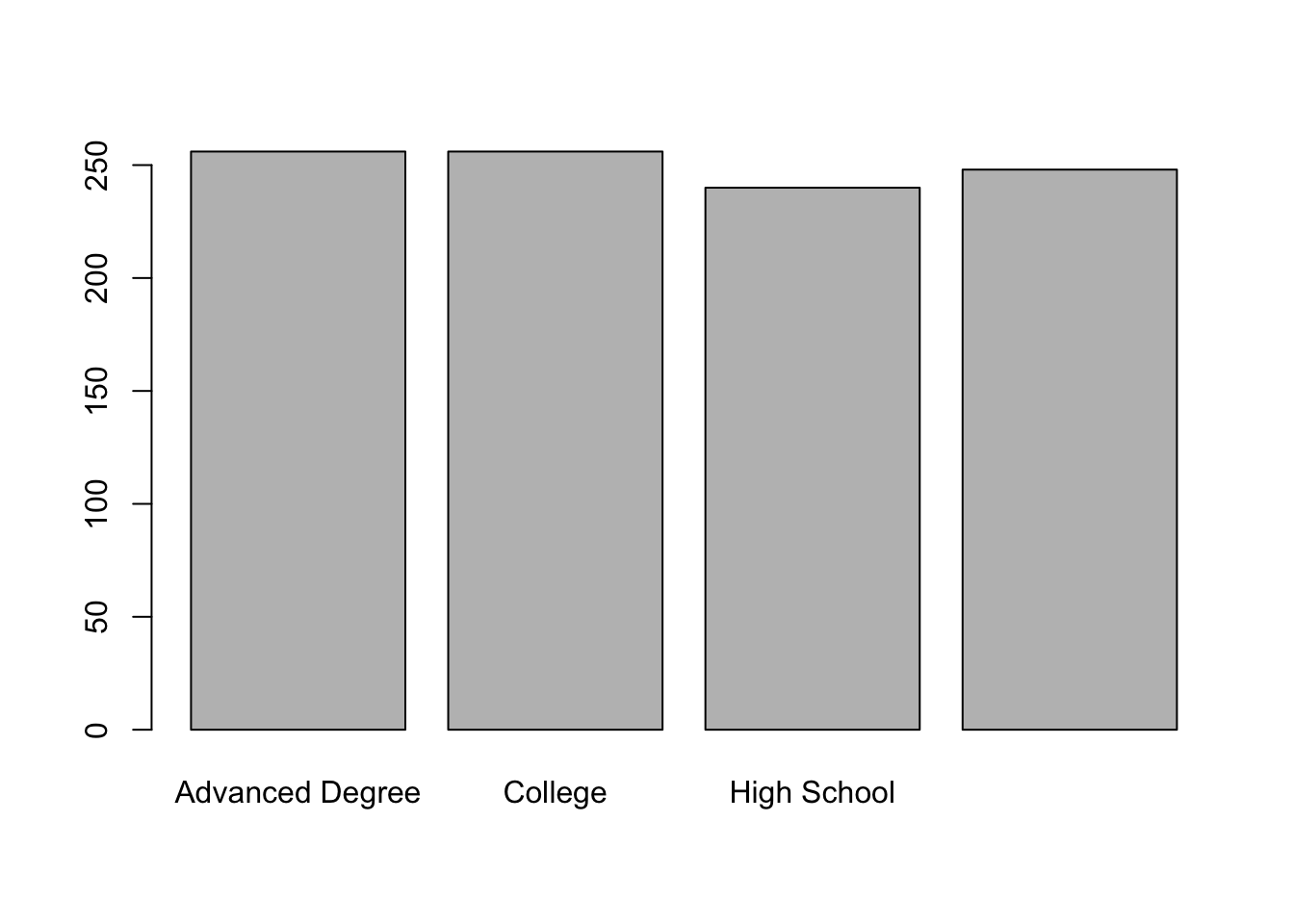
What’s the problem with this chart?? The bars aren’t in the right order! We would never want to present this like this, and we will learn how to change this in a future class. (It’s converting this to a factor variable, which we well get to).
The fourth type of variable is continuous. This is a variable that can take on any number in our number system. An example of this is income:
head(income)
#> [1] 82792.42 92237.33 86164.46 49175.03 107769.36
#> [6] 40778.60We can take the mean, median, and find the standard deviation of this variable:
mean(income)
#> [1] 89646.77
median(income)
#> [1] 88110.6
sd(income)
#> [1] 34257.24
summary(income)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 30030 60269 88111 89647 119933 149968Can we use table() with this variable? What does table() do? It tells us the relative frequency of different possibilities. What will that look like here?
#table(income)Garbage! All of the incomes are unique values, so we just get a table telling us that there is 1 of each value. This is useless.
How do we want to visualize a continuous variable? With these types of variables we want to visualize both the overall level of the variable as well as the dispersion/spread of the variable.
Why is this second thing important? Well, here the mean income is around $90k. But that alone doesn’t really tell us what kind of population it is. Maybe everyone has around $90k. Maybe income is pretty evenly spread out where some people have $30k, some people have $150k. Maybe most people have $10k and one guy has a billion dollars. Just knowing the mean, all are possible!
So how can we visualize this dispersion? The first option is to use a boxplot:
boxplot(income)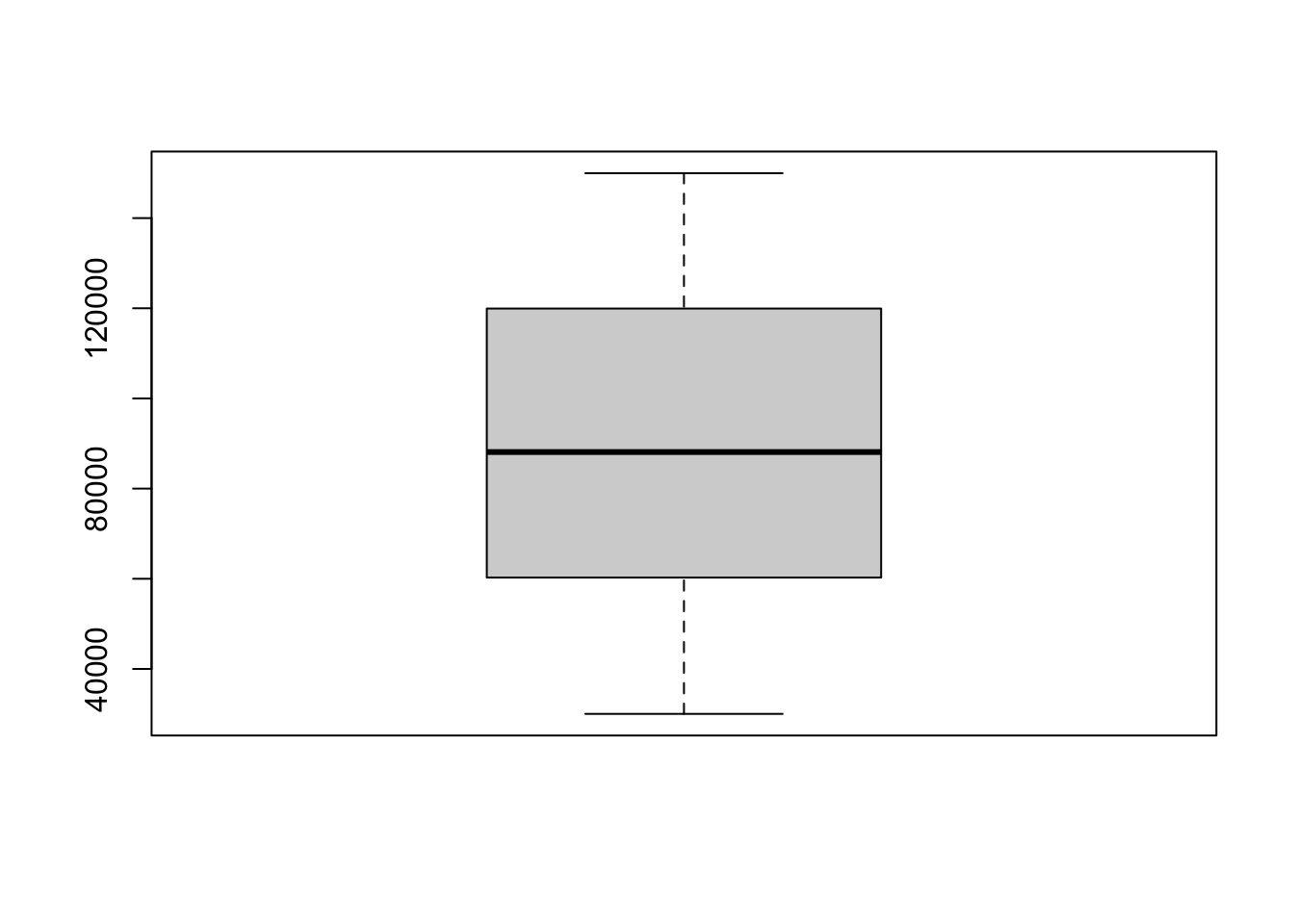
The boxplot shows the same info as summary(). The dark line in the middle is the median, the box covers the 25th to 75th percentiles, and the two “whiskers” are the min and max values.
The other possibility for visualizing a single continuous variable is a density chart. If we just run the command density() we get the information to make this chart, but it’s not very helpful or readable on it’s own:
density(income)
#>
#> Call:
#> density.default(x = income)
#>
#> Data: income (1000 obs.); Bandwidth 'bw' = 7745
#>
#> x y
#> Min. : 6797 Min. :9.029e-09
#> 1st Qu.: 48398 1st Qu.:2.826e-06
#> Median : 89999 Median :7.913e-06
#> Mean : 89999 Mean :5.997e-06
#> 3rd Qu.:131601 3rd Qu.:8.447e-06
#> Max. :173202 Max. :9.275e-06But if we wrap that command in plot() we get something much more helpful:
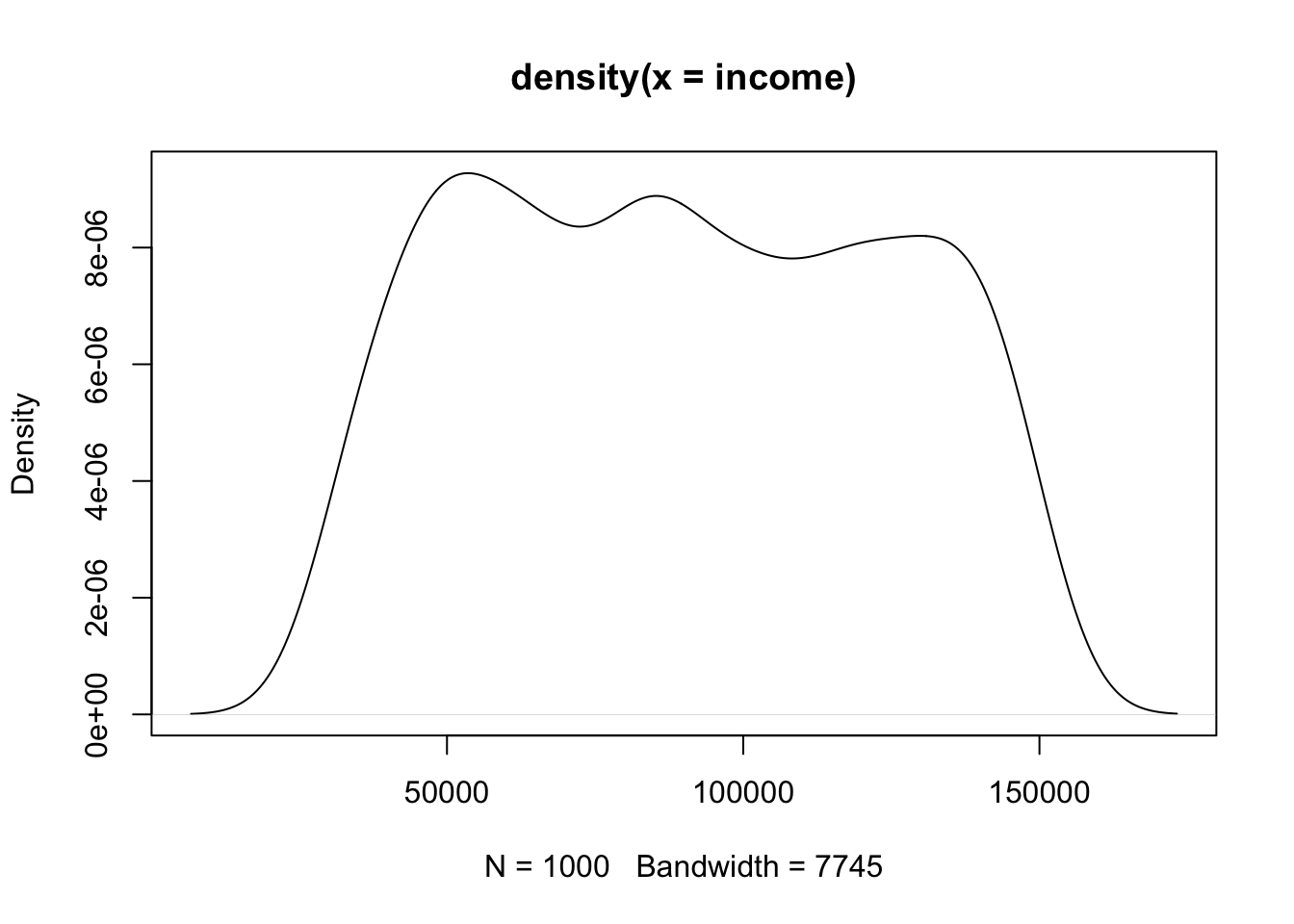
We can think about a density plot as a continuous histogram. The different possible values for our variable are on the x-axis, and the height of the line at that point is the relative frequency of data around that point.
So applying this to our population.table, how would we plot emmissions?
population.table
#> year world.pop pop.rate emissions
#> [1,] 1950 2525 1.000000 6.00
#> [2,] 1960 3026 1.198416 9.33
#> [3,] 1970 3691 1.461782 14.83
#> [4,] 1980 4449 1.761980 19.37
#> [5,] 1990 5320 2.106931 22.70
#> [6,] 2000 6127 2.426535 25.12
#> [7,] 2010 6916 2.739010 33.13This is a continuous variable (it can take on any number), so we would want to use a boxplot or density plot:
boxplot(population.table[,4])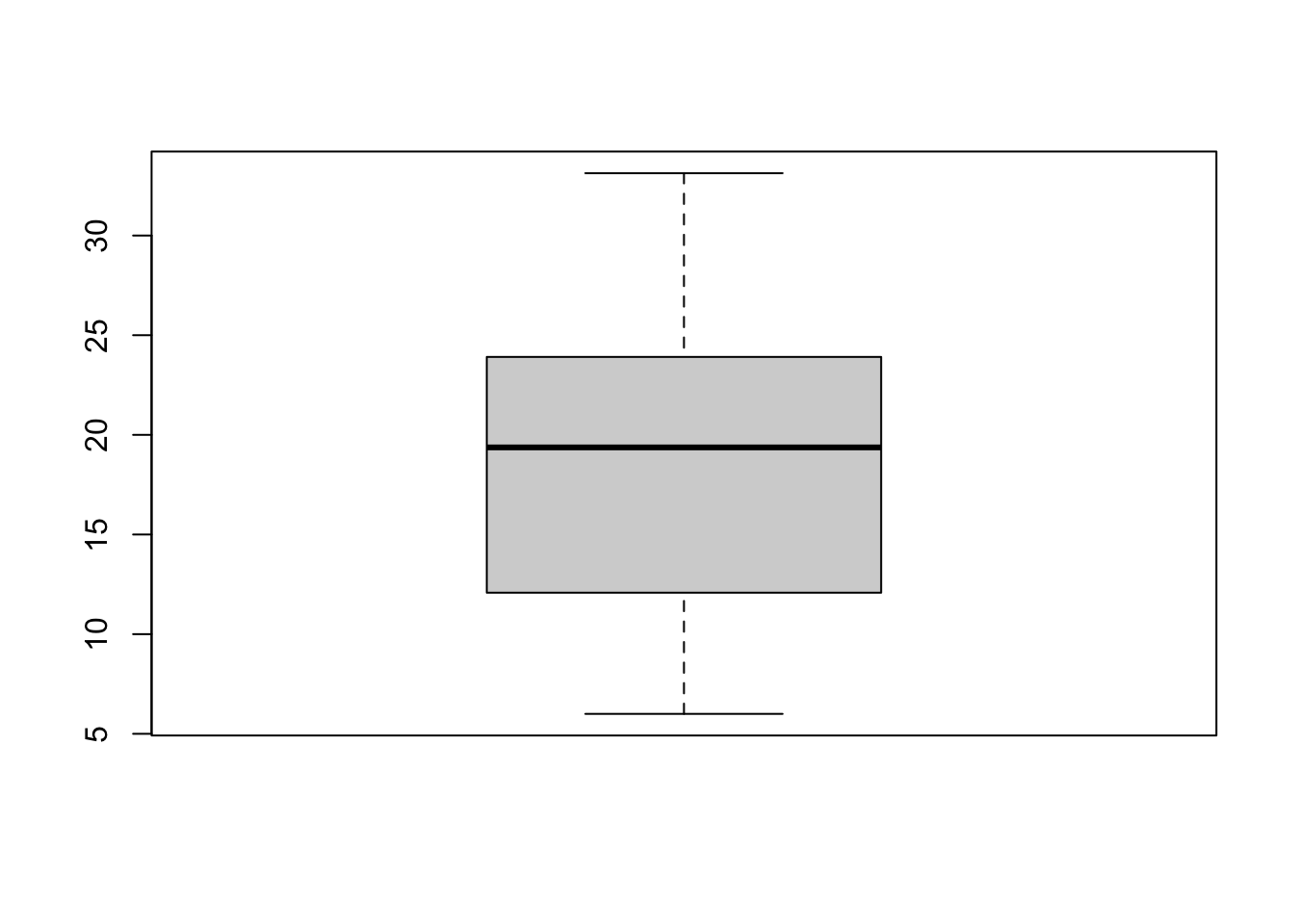
Plotting one variable at a time is fine, but often what we want to look at is the relationships between two variables.
Again, when doing this we want to think about the variable types when doing this. The type of graph will change based on whether we are visualizing two categorical variables, or two continuous, or a continuous and a categorical variable etc.
For today, let’s consider having two continuous variables.
What if we want to graph a scatter plot with year on the x (horizontal) axis and the world population on the y (vertical) axis.
We want a scatterplot here: a plot that has a dot for each combination of year and world population. To get a scatterplot we use the basic plot() command.
#?plotWen we run a scatterplot, the first two “options” of the command will be our x (horizontal) and y (vertical) pieces of data. Here year is the first column of our dataset and world.pop is the second:
plot(population.table[,1], population.table[,2])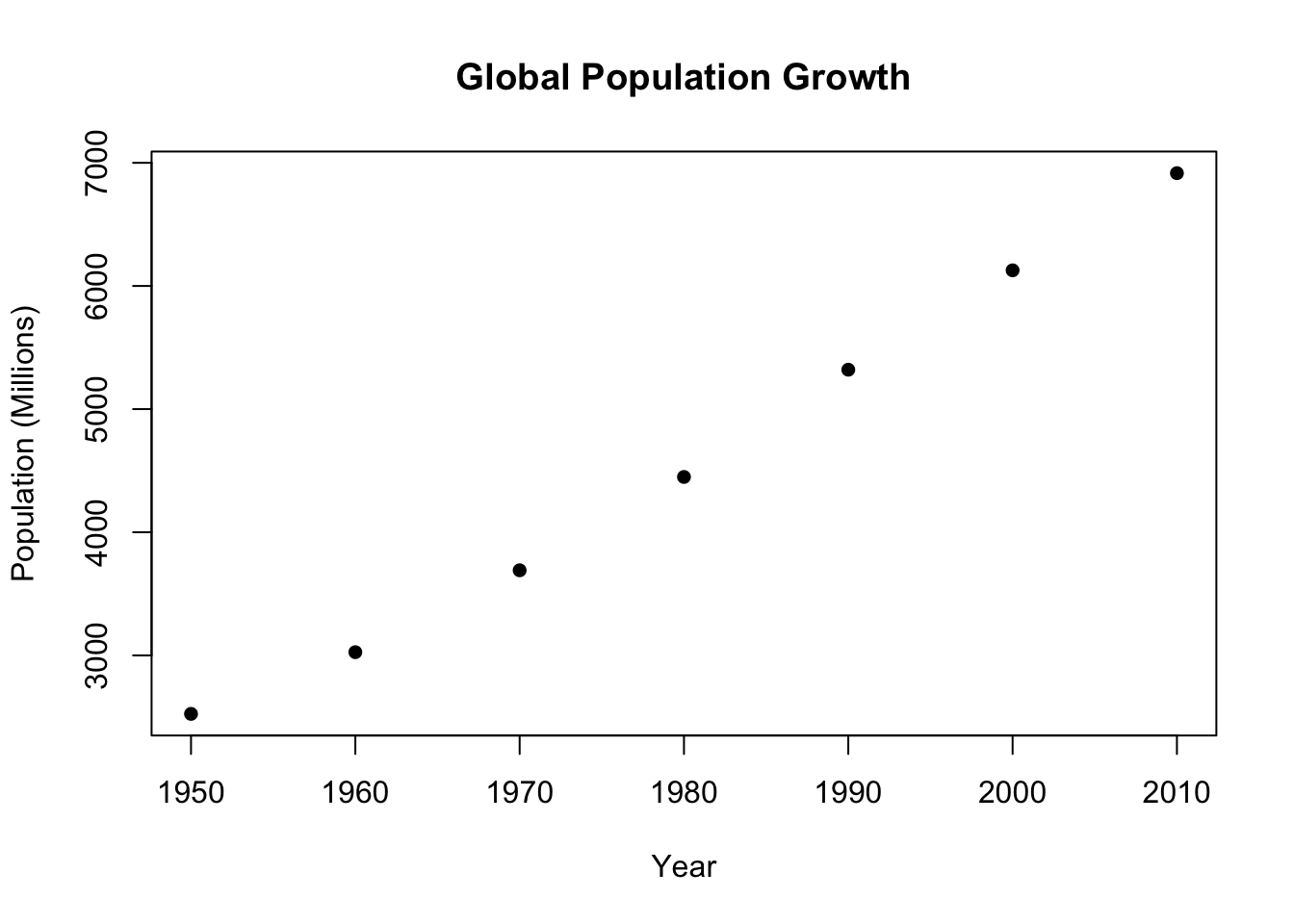
Because we are giving R two pieces of information for each dot (it’s horizontal and vertical position) the two vectors we feed the plot command must be the same length.
If we uncomment and try to run the following:
#plot(population.table[,1], population.table[-1,2])We get a very straight-forward error.
The graph we made is fine, but it’s not something I would be happy presenting. How can we add some bells and whistles like titles? Some of these things are options in the plot command:
plot(population.table[,1], population.table[,2],
main="Global Population Growth",
xlab="Year",
ylab="Population (Millions)")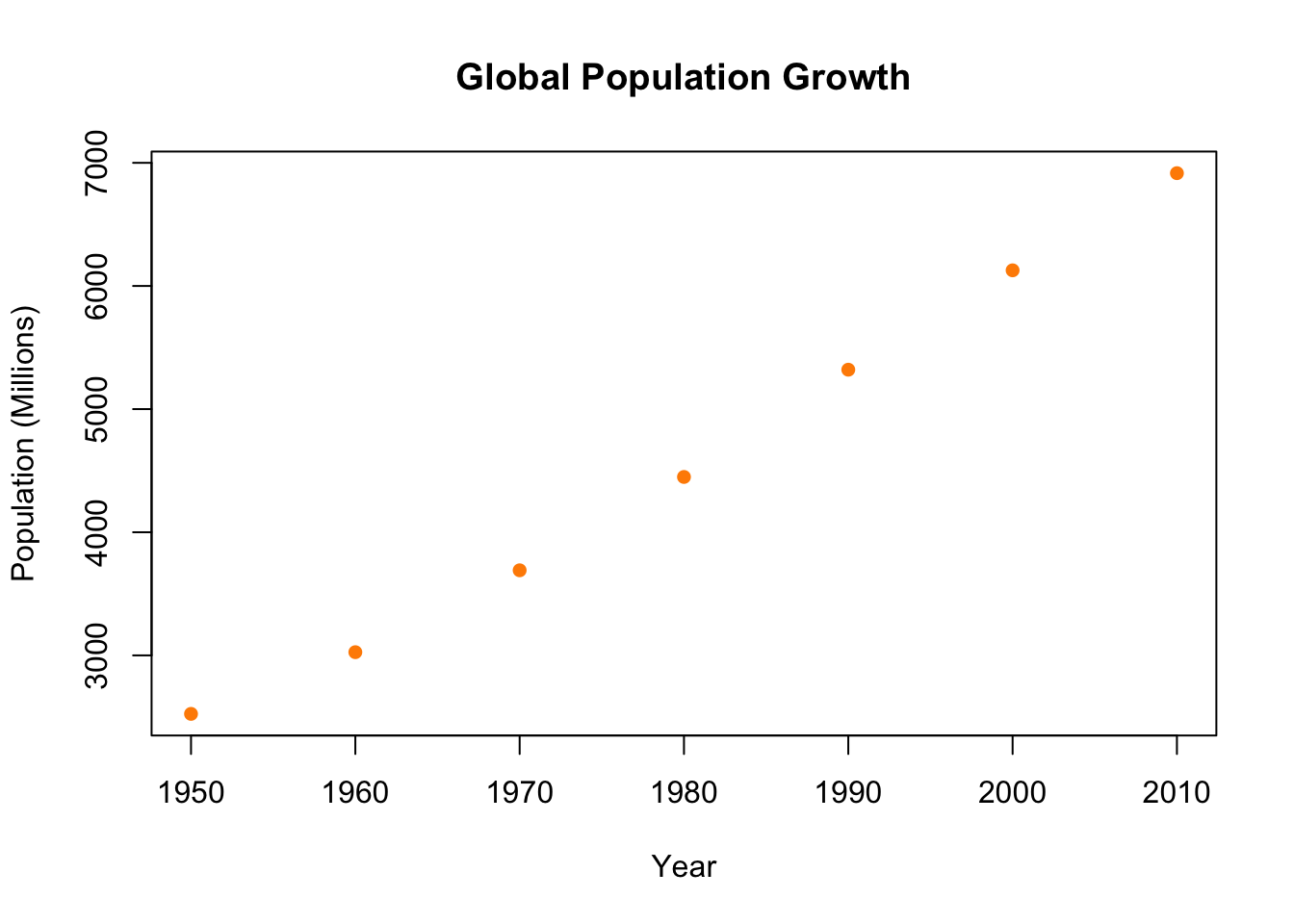
I’m not a big fan of these hollow dots, but we can easily change the point type to something else:
plot(population.table[,1], population.table[,2],
main="Global Population Growth",
xlab="Year",
ylab="Population (Millions)",
pch=16)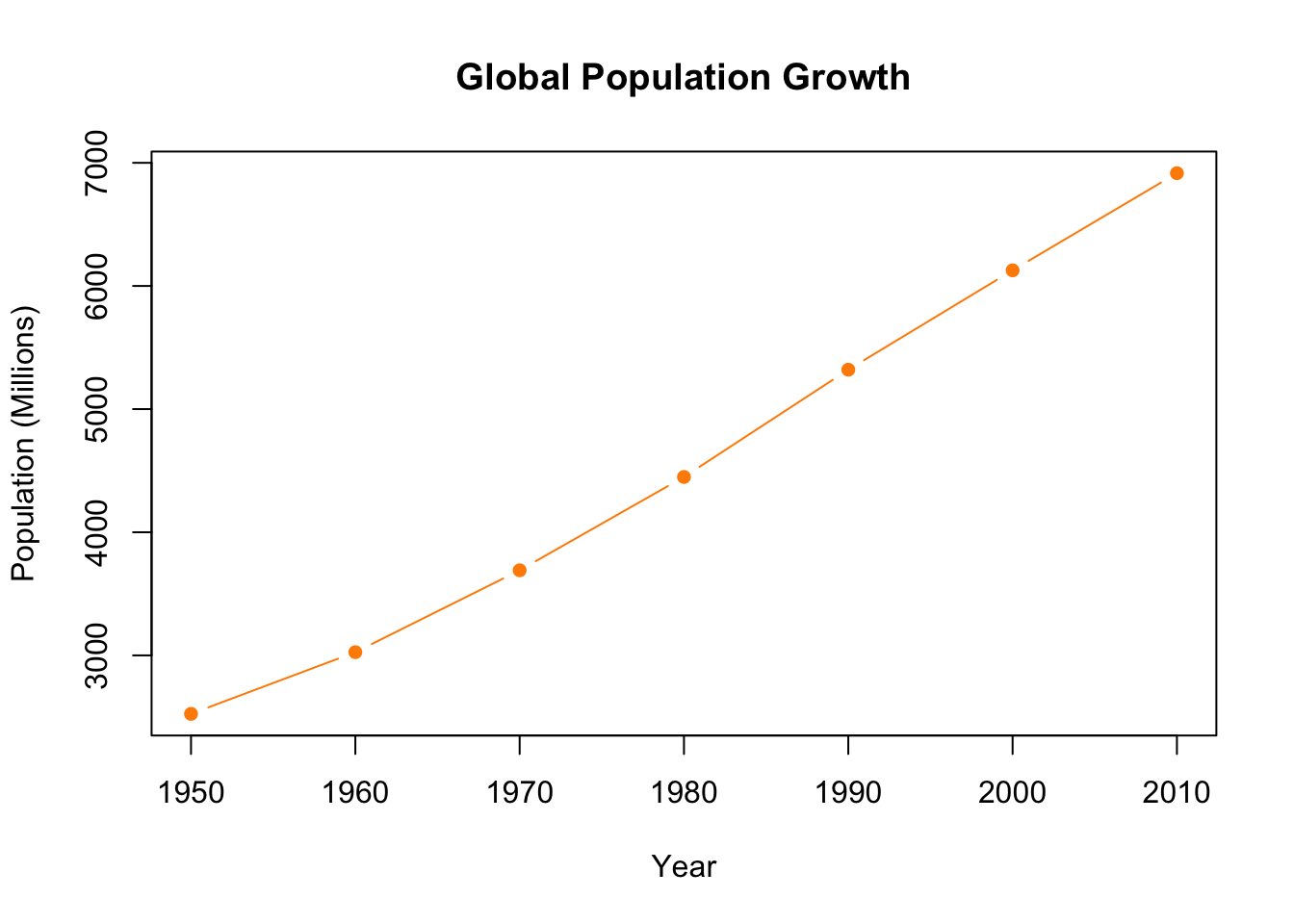
If you are curious, here are all the point types:
We can also add some color:
plot(population.table[,1], population.table[,2],
main="Global Population Growth",
xlab="Year",
ylab="Population (Millions)",
pch=16,
col="darkorange")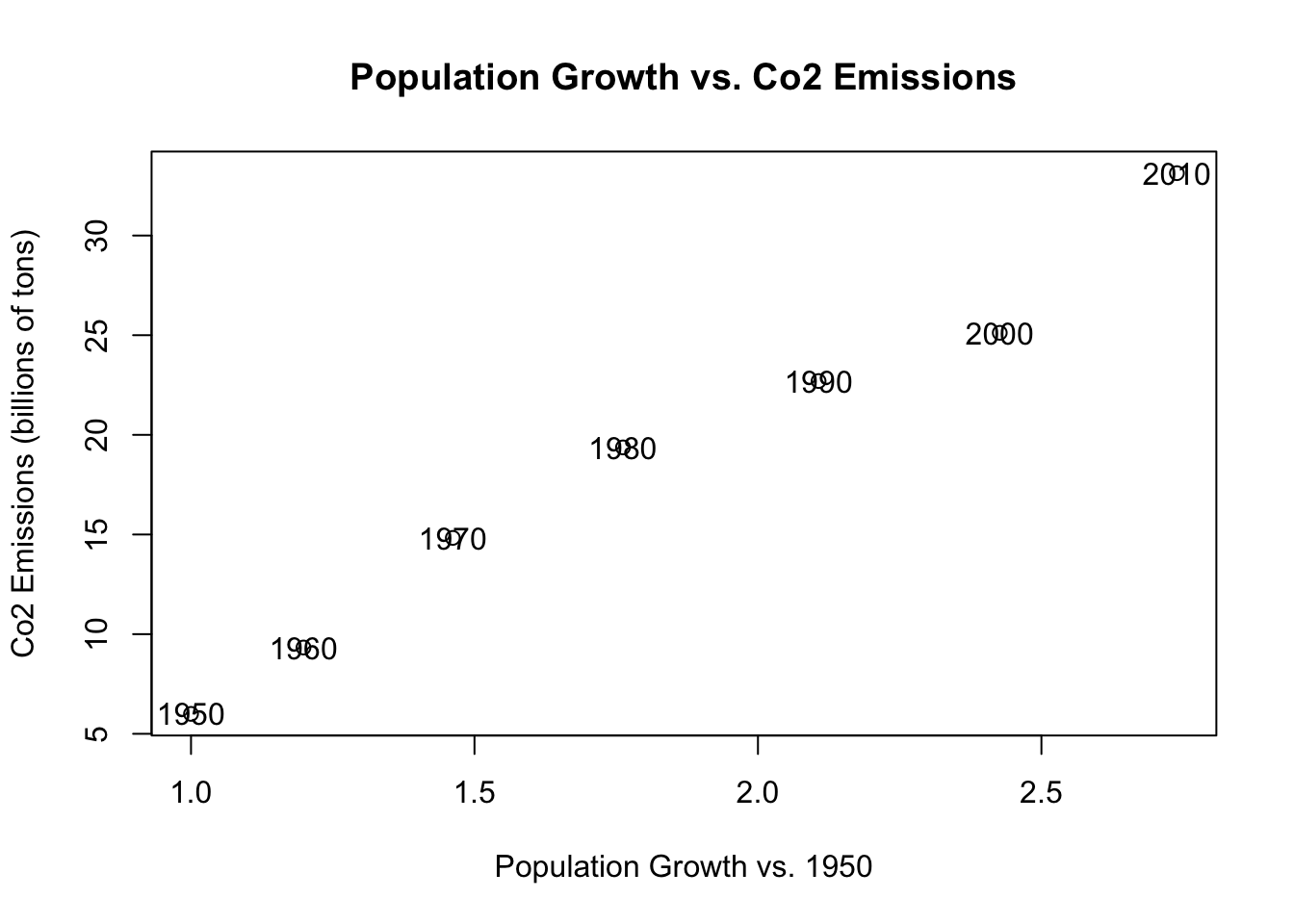
Here is a webpage with all the possible R colors. (You can also make your own custom colors if you are into that.)
What if we want these points to be connected? That’s appropriate in this case because this is a “series” of data. Each data point logically follows the next in the dataset.
The graph “type” will give you different options where:
p = points
l = line
b = both
n = none
p is the default, so you want points you don’t actually have to do anything. But to get connecting points we can do:
plot(population.table[,1], population.table[,2],
main="Global Population Growth",
xlab="Year",
ylab="Population (Millions)",
pch=16,
col="darkorange",
type="b")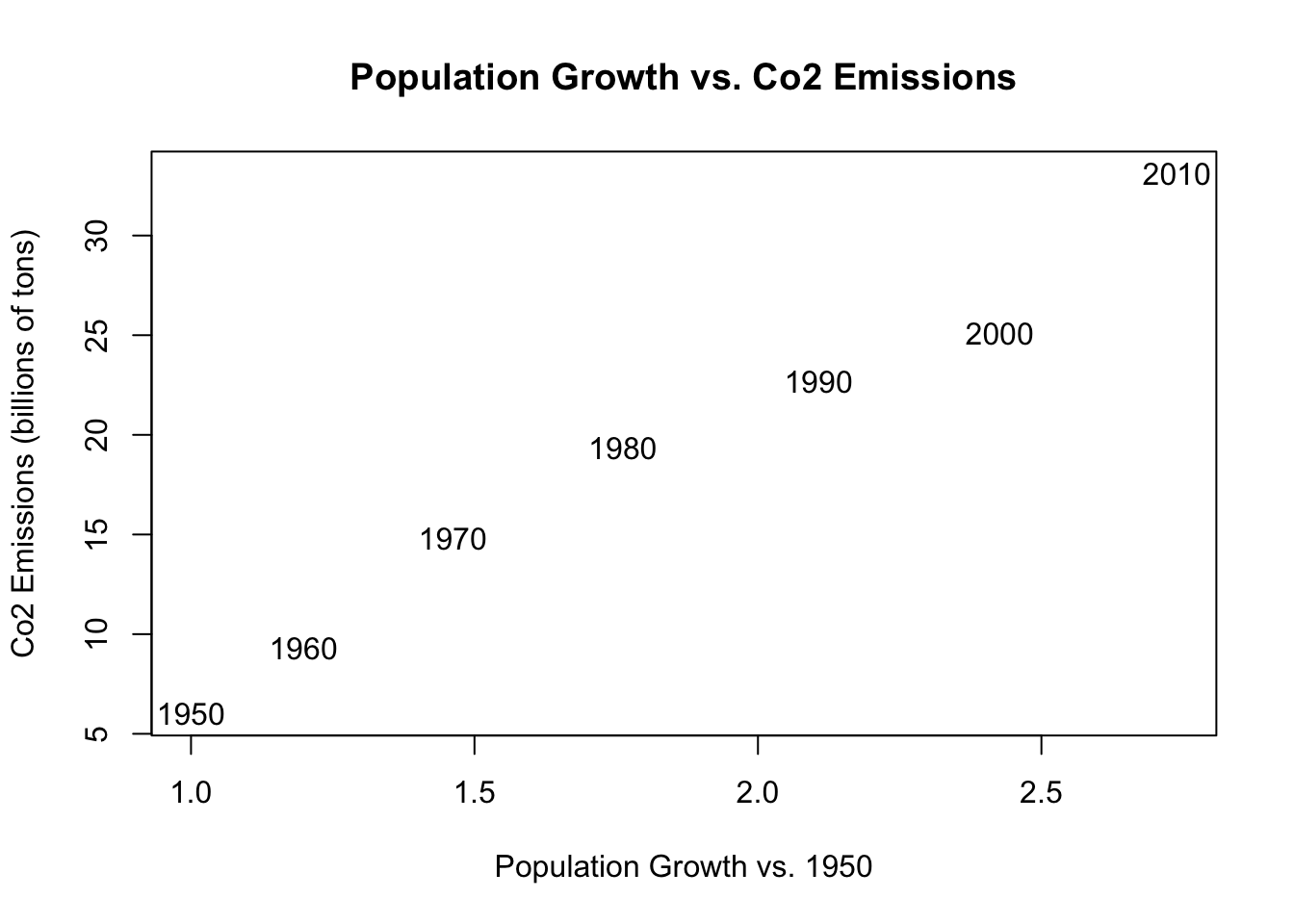
Why would we ever want “n”??
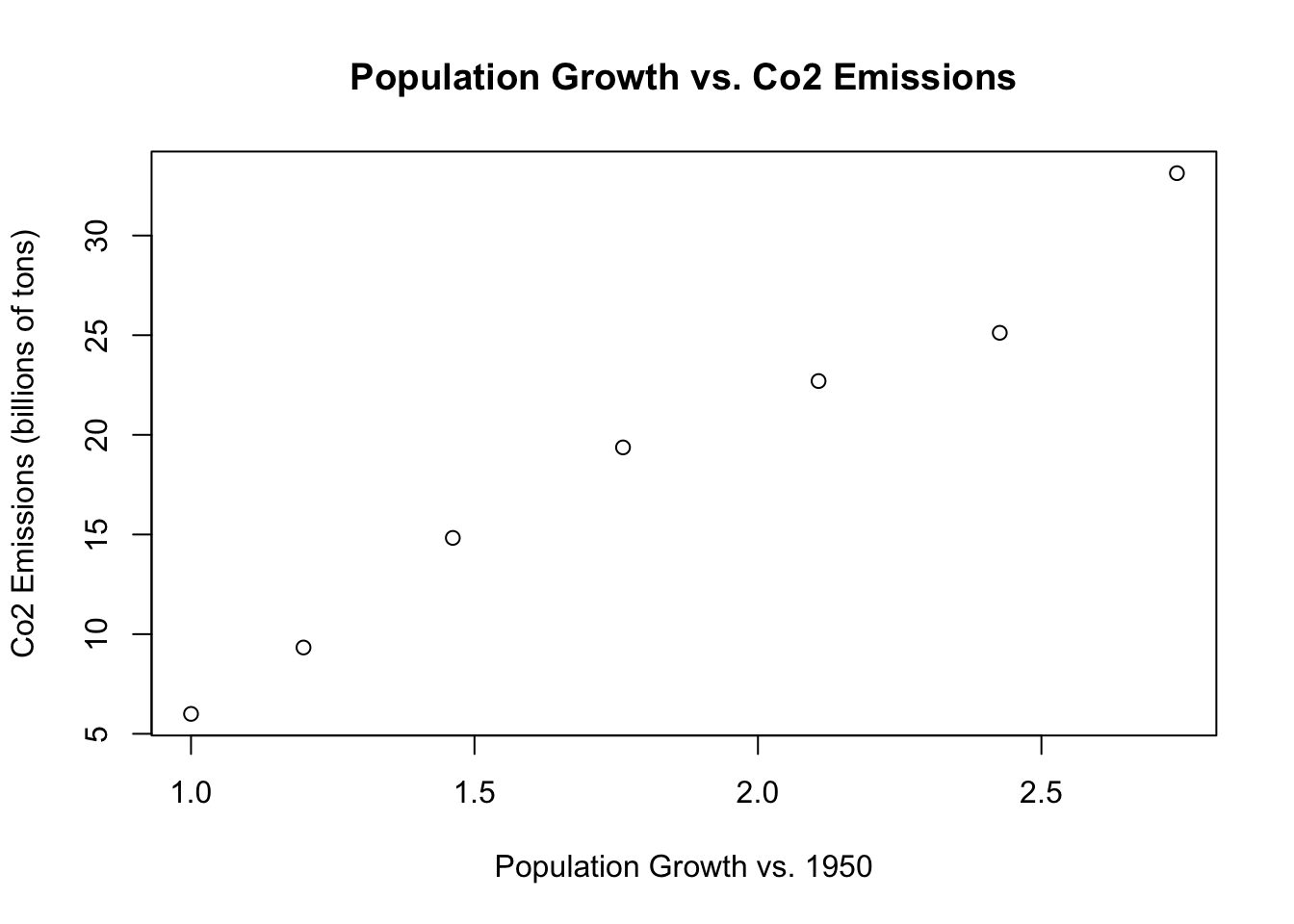
Let’s consider a second graph with population rate on the x-axis and emissions on the y-axis. Instead of points, we want each “dot” to be the year:
plot(population.table[,3], population.table[,4],
xlab="Population Growth vs. 1950",
ylab="Co2 Emissions (billions of tons)",
main="Population Growth vs. Co2 Emissions")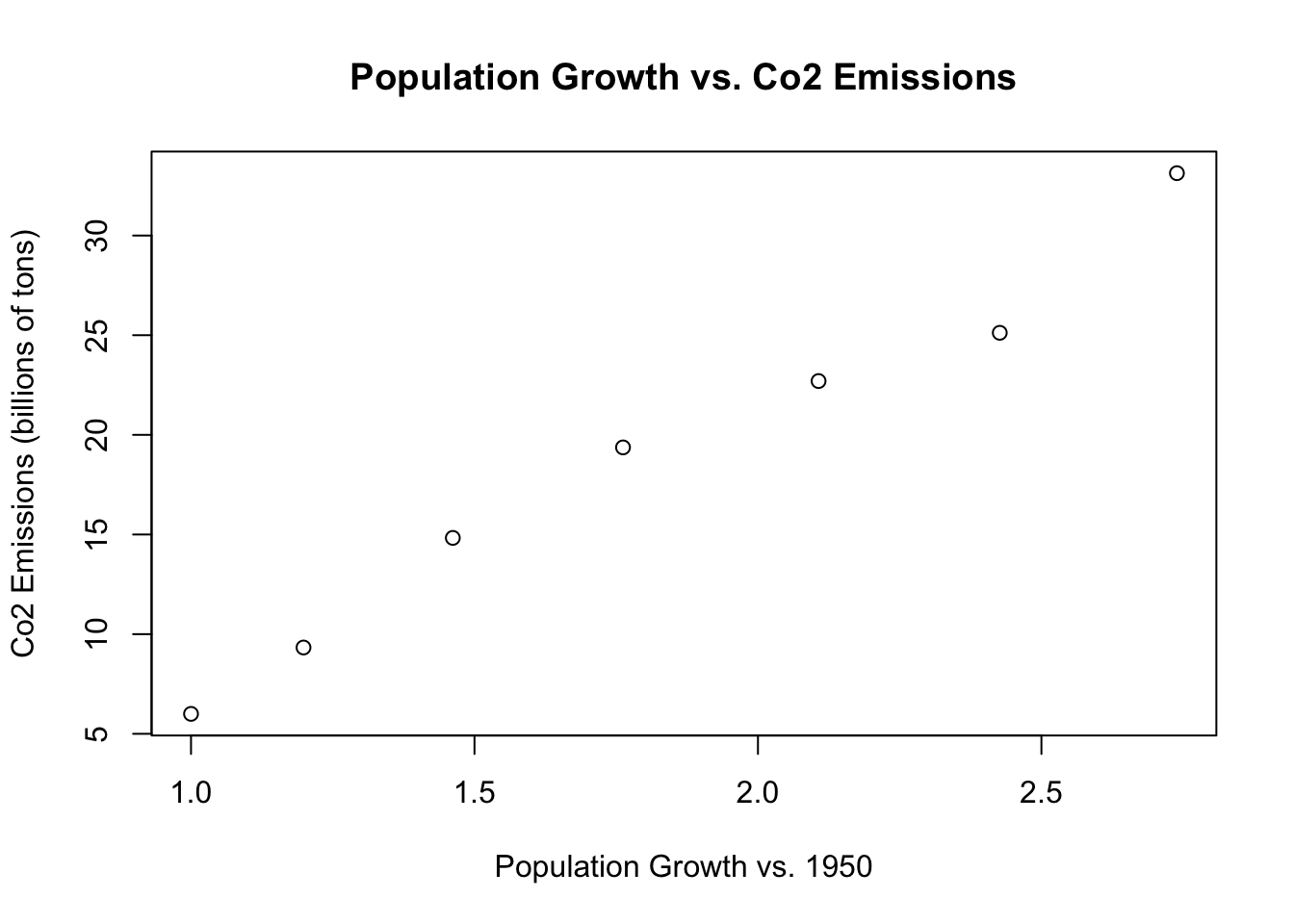
The nice thing about graphing in R is that we can “draw” additional information on the same graph once an initial plot() command has been run. We can draw additional points, or lines, and in this case, text.
We can use the text command to put a vector of text at a certain location.
plot(population.table[,3], population.table[,4],
xlab="Population Growth vs. 1950",
ylab="Co2 Emissions (billions of tons)",
main="Population Growth vs. Co2 Emissions")
text(population.table[,3], population.table[,4],
labels=population.table[,1])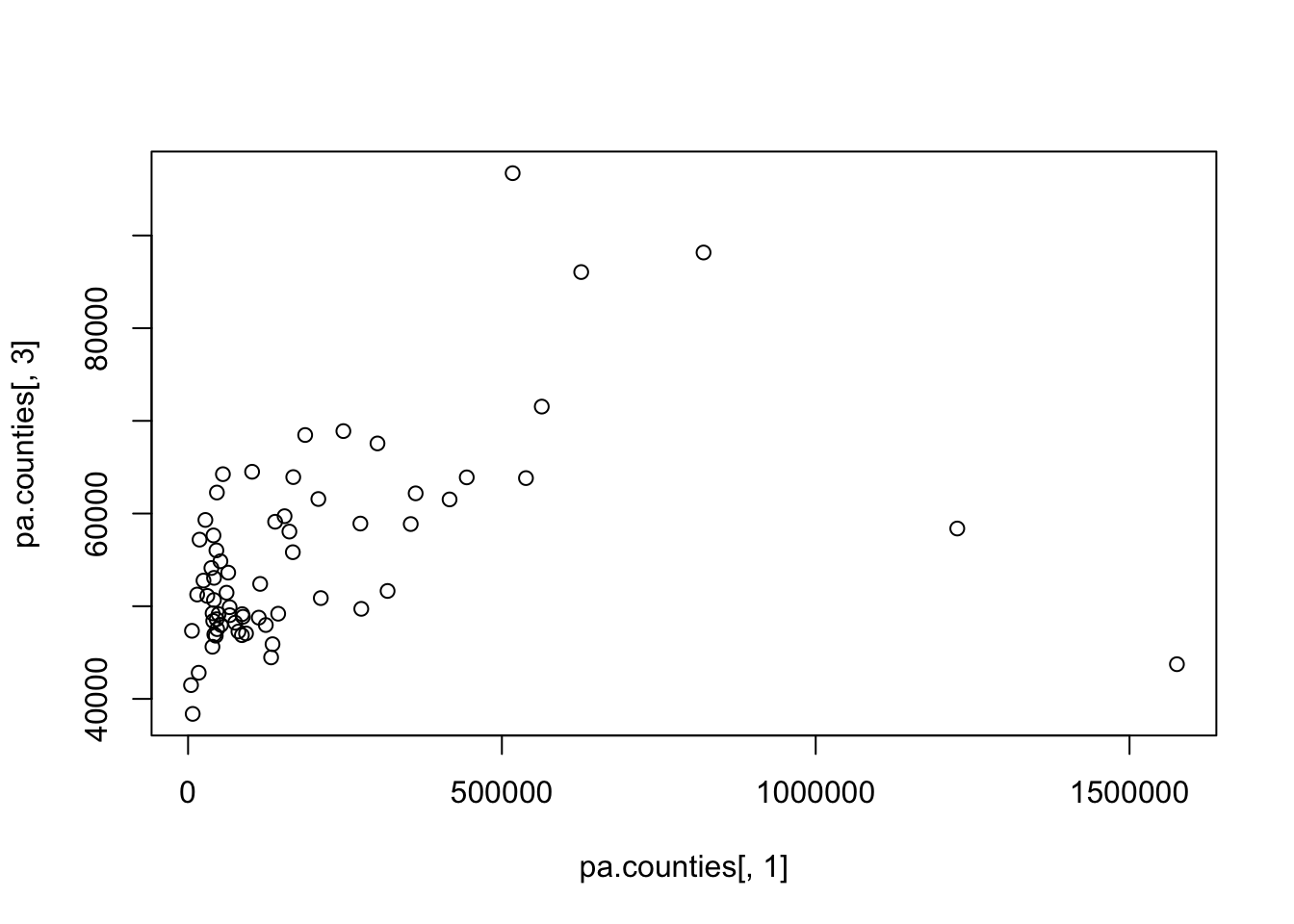
But now we have these years overlapping the dots which looks bad, So we can use type=“n” to remove those dots:
plot(population.table[,3], population.table[,4],
xlab="Population Growth vs. 1950",
ylab="Co2 Emissions (billions of tons)",
main="Population Growth vs. Co2 Emissions",
type="n")
text(population.table[,3], population.table[,4],
labels=population.table[,1])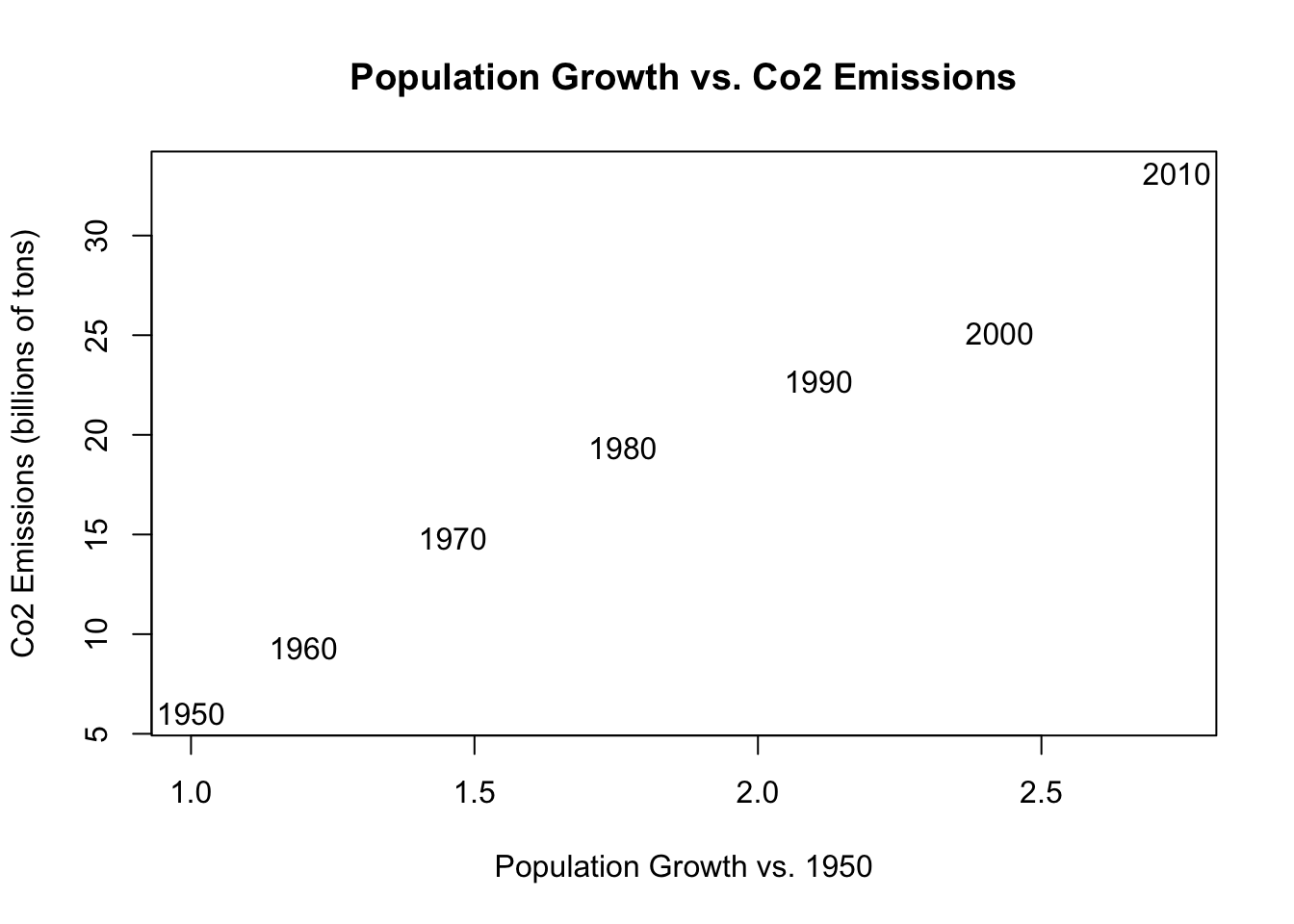
Let’s do another example. pa.counties is a data table containing some information about counties in Pennsylvania. We can see in the environment in the top right of r-studio that pa.counties is a matrix with 5 columns and 67 rows. That’s too much information to display in the console, so we can use the head() command to display the first 6 rows:
head(pa.counties)
#> population population.density median.income
#> [1,] 61304 53.42781 51457
#> [2,] 626370 1036.30200 86055
#> [3,] 123842 235.53000 47969
#> [4,] 41806 42.69485 46953
#> [5,] 112630 167.45910 48768
#> [6,] 46362 112.79050 47526
#> percent.college percent.transit.commute
#> [1,] 17.84021 0.2475153
#> [2,] 40.46496 3.4039931
#> [3,] 20.80933 1.1913318
#> [4,] 18.14864 0.9152430
#> [5,] 22.55270 0.4175279
#> [6,] 12.47843 0.3038048How might we visualize the relationship between the population of a county and the median income of that county?
#Basic
plot(pa.counties[,1], pa.counties[,3])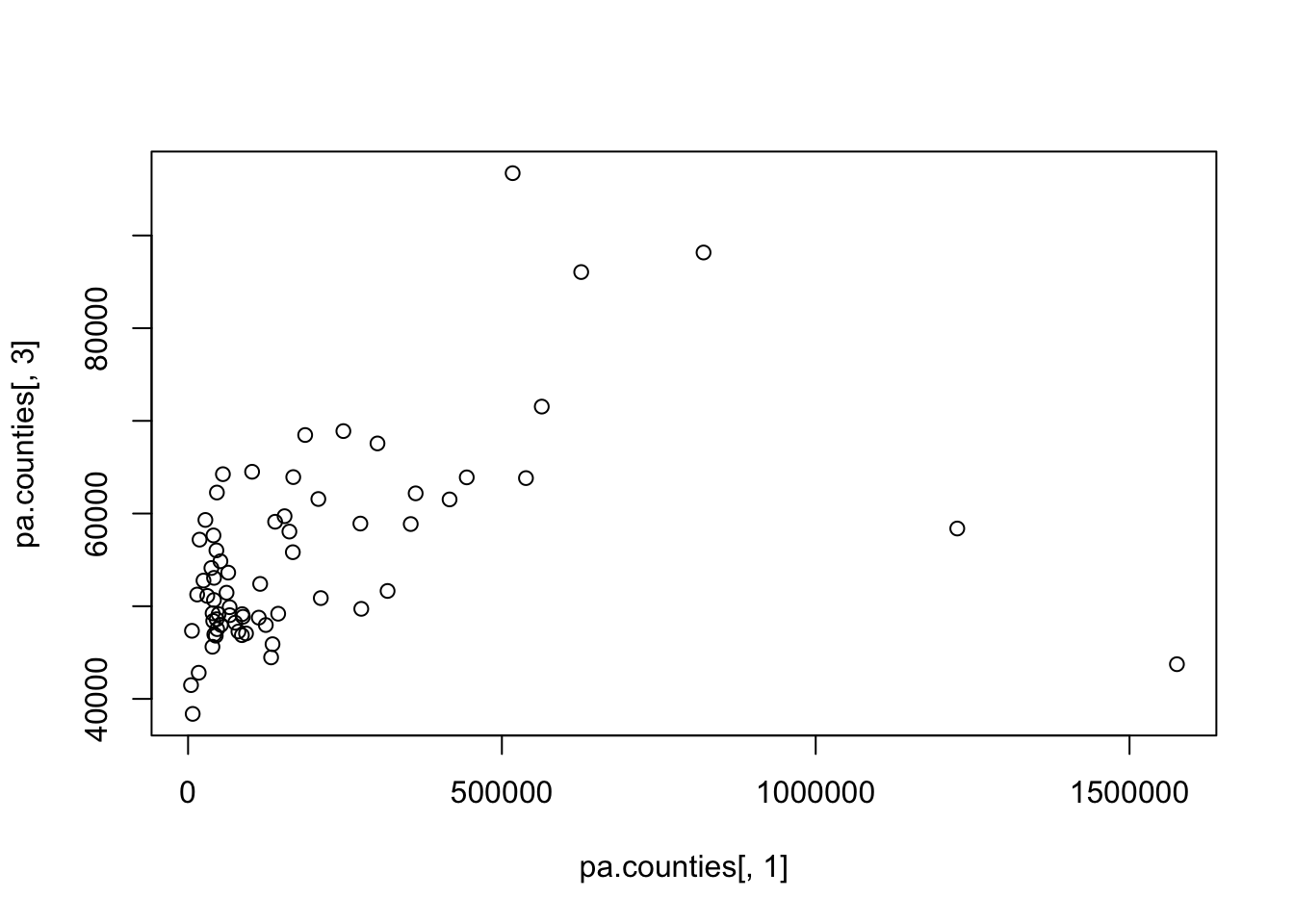
#Full Graph
plot(pa.counties[,1], pa.counties[,3],
main="Relationship between Population and Median Income in PA",
xlab="Population",
ylab="Median Income",
pch=16,
col="Darkblue")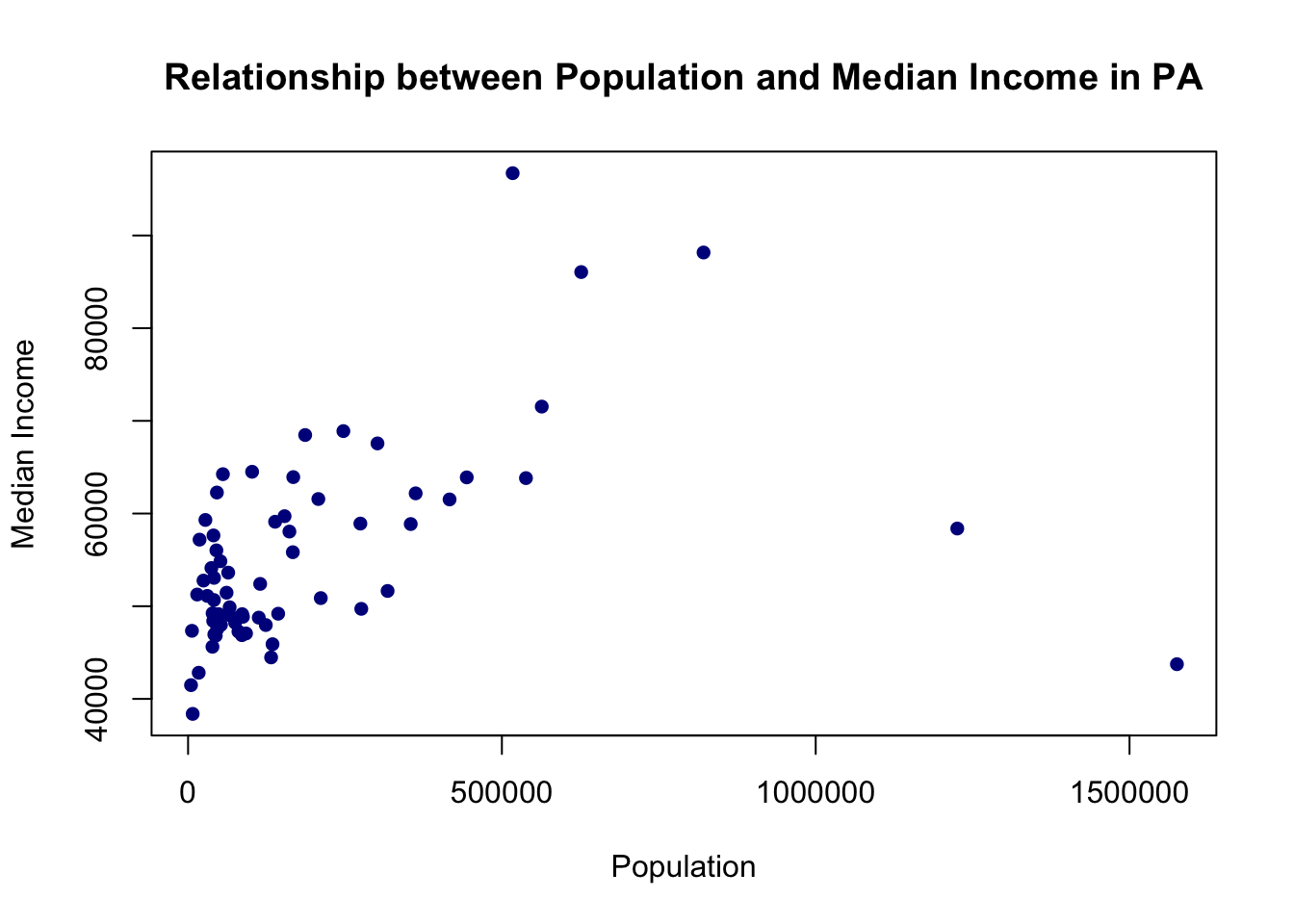
What would you say about the relationship? Why is type “l” or “b” wrong here (you should try those types to see).